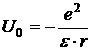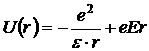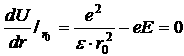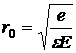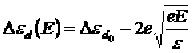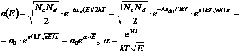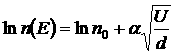Лекции для студентов

Физика полупроводников. Лекция 4

§7. Термоэлектронная ионизация Френкеля.

В сильных электрических полях концентрация носителей заряда может возрастать в результате различных механизмов, основными из которых являются: эффект термоэлектронной ионизация Френкеля, эффект ударной ионизации, туннельный эффект (электростатическая ионизация Зинера).

Эффект термоэлектронной ионизация Френкеля связан с уменьшением в сильных электрических полях энергии ионизации мелких примесей, которые ответственны за равновесную концентрацию носителей заряда. Для определенности будем полагать, что полупроводник имеет мелкие центры донорного типа. Орбита валентных электронов таких центров охватывает несколько постоянных решеток. Поэтому взаимодействие электрона со своим ионом экранируется связанными зарядами, образующимися в результате поляризации решетки (водородо подобная модель). Тогда потенциальная энергия валентного электрона мелкого донора в отсутствии внешнего электрического поля имеет вид:

(1)

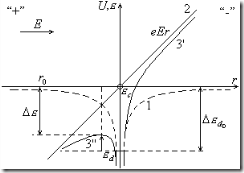На рисунке показан ход потенциала (1). Кривая 1 отображает распределение потенциала в соответствии 1 формулой (1). , ; ,

, при , и если , то

соответствуют связанные состояния валентного электрона донора, состояние свободного состояния.  — энергия ионизации донора.

Теперь приложим к полупроводнику донорного типа внешнее электрическое поле, так как показано на рисунке. Прямой 2 обозначен ход потенциальной энергии электрона во внешнем электрическом поле. Она будет возрастать в направлении поля и уменьшаться в направлении против поля. Потенциальная энергия алгебраически складывается. Сложим кривые 1 и 2, т.е. найдем распределение суммарного потенциала электрона. Видно, что потенциальный барьер в направлении поля увеличивается, а в направлении против поля — уменьшается (кривая 3''). Видно, что потенциальный барьер для валентного электрона донора уменьшается на величину . Энергия ионизации в присутствии внешнего поля равна:

Найдем . Для этого найдем координату точки для максимального потенциала. Очевидно, суммарная потенциальная энергия валентного электрона равна:

В первом слагаемом этого соотношения , а во втором слагаемом входит со своим знаком. Справа рисунка положительна, а слева отрицательна. Возьмем производную по от функции и приравняем к нулю.

,

Очевидно, равно абсолютному значению функции в точке :

Значит, энергия ионизации мелких доноров во внешнем электрическом поле рана:

Известно, что в донорном некомпенсированном полупроводнике при низких температурах концентрация свободных электронов равна:

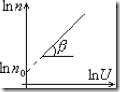
Прологарифмируем n:

,

 — толщина полупроводника или расстояние между контактами,  — приложенное напряжение.

Термоэлектронная ионизация Френкеля наблюдается в электрических полях

Этот эффект имеет место при низких температурах, когда концентрация неионизированных доноров значительно больше, чем ионизированных, т.е. когда