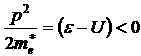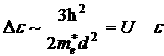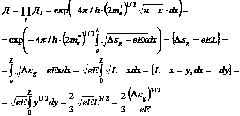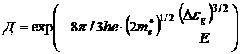Физика полупроводников. Лекция 4
- Физика полупроводников. Лекция 4
- §2. Дрейфовая электропроводность в полупроводнике.
- §3. Диффузионная электропроводность в полупроводнике. Соотношения Эйнштейна.
- §4. Температурная зависимость подвижности носителей заряда в полупроводниках.
- §5. Температурная зависимость подвижности при смешанном механизме рассеяния носителей заряда.
- §6. Разогрев носителей заряда в сильных электрических полях.
- §7. Термоэлектронная ионизация Френкеля.
- §8. Ударная ионизация в полупроводниках.
- §9. Туннельный эффект в полупроводниках (электростатическая ионизация Зинера).
- §10. Отрицательная дифференциальная проводимость (ОДП) полупроводников с двух долинной зонной структурой.
- §11. Колебания тока в двухдолинных полупроводниках (эффект Ганна).
- §12. Токи ограниченные пространственным зарядом (ТОПЗ) в полупроводниках без “ловушек”.
- §13. ТОПЗ в полупроводниках с ловушками.
- §14. Основные свойства сверхпроводящего состояния твердых тел.
- §15. Природа сверхпроводимости (теория БКШ).
- §16. Применение сверхпроводимости.
§9. Туннельный эффект в полупроводниках (электростатическая ионизация Зинера).
Может наблюдаться в электрических полях 
. Если энергия электрона 
то классический электрон не может попасть внутрь такого барьера, так как в этом случае кинетическая энергия равна:
импульс — мнимый. Но с квантовой точки зрения электрон с такими энергетическими параметрами может просочиться сквозь потенциальный барьер, проходя его без изменения своей энергии (туннельный эффект). Туннельный эффект может быть объяснен соотношением неопределенности:
Фиксация электрона внутри барьера 
приводит к неопределенности импульса электрона и его кинетической энергии:
, 
Очевидно, туннельное просачивание возможно, если неопределенность кинетической энергии равна:
Туннельный эффект характеризуется коэффициентом прозрачности барьера Д, он равен отношению числа частиц прошедших сквозь барьер к числу частиц падающих на барьер. Для барьера прямоугольной формы:
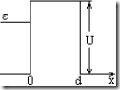
В сильных электрических полях (крутой наклон зон) возможны туннельные переходы электронов с донорных центров в зону проводимости или из валентной зоны в зону проводимости. Рассмотрим туннельный эффект электронов из валентной зоны в зону проводимости. Такой электрон туннелирует сквозь потенциальный барьер треугольной формы.
Будем рассматривать туннелирование валентного электрона, имеющего энергию 
. Он туннелирует из точки O в точку L. Потенциальный барьер OAL имеет треугольную форму, Высота его U. Аппроксимируем этот треугольный барьер суммой узких прямоугольных барьеров. Например, для i барьера, ширина которого dx, коэффициент прозрачности будет:
Высота i барьера 
. 
, 
ширина треугольного барьера. Очевидно, коэффициент треугольного барьера равен:
(1)
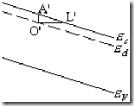Из (1) следует, что вероятность туннельного просачивания электронов из валентной зоны в зону проводимости экспоненциально возрастает с напряженностью электрического поля и тем быстрее, чем меньше 
и 
. Расчеты показывают, что при 
и 
межзонное туннелирование начинается при 
. При меньших электрических полях возможно туннелирование электронов с донорных уровней через треугольный барьер. В этом случае коэффициент прозрачности будет равен:
С квантовой точки зрения туннелирование возможно при условии, когда длина электронной волны соизмерима с шириной потенциального барьера. А ширину потенциального барьера можно варьировать величиной электрического поля (чем больше поле, тем меньше ширина потенциального барьера: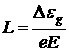 
).
