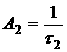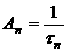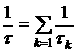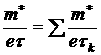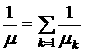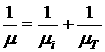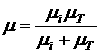Физика полупроводников. Лекция 4
- Физика полупроводников. Лекция 4
- §2. Дрейфовая электропроводность в полупроводнике.
- §3. Диффузионная электропроводность в полупроводнике. Соотношения Эйнштейна.
- §4. Температурная зависимость подвижности носителей заряда в полупроводниках.
- §5. Температурная зависимость подвижности при смешанном механизме рассеяния носителей заряда.
- §6. Разогрев носителей заряда в сильных электрических полях.
- §7. Термоэлектронная ионизация Френкеля.
- §8. Ударная ионизация в полупроводниках.
- §9. Туннельный эффект в полупроводниках (электростатическая ионизация Зинера).
- §10. Отрицательная дифференциальная проводимость (ОДП) полупроводников с двух долинной зонной структурой.
- §11. Колебания тока в двухдолинных полупроводниках (эффект Ганна).
- §12. Токи ограниченные пространственным зарядом (ТОПЗ) в полупроводниках без “ловушек”.
- §13. ТОПЗ в полупроводниках с ловушками.
- §14. Основные свойства сверхпроводящего состояния твердых тел.
- §15. Природа сверхпроводимости (теория БКШ).
- §16. Применение сверхпроводимости.
§5. Температурная зависимость подвижности при смешанном механизме рассеяния носителей заряда.
Как уже отмечалось, кристаллы могут содержать несколько типов рассеивающих центров. Каждый такой тип рассеивающих центров характеризуется своей вероятностью рассеяния.
, 
, 
…
— времена рассеяния, связанные с соответствующими типами центров. Если бы в кристалле содержался только один тип например k центров, то подвижность была бы равна:
.
С увеличением числа типов центров рассеяния увеличивается вероятность рассеяния носителей заряда. Вероятность сложного события равна сумме вероятностей не зависимых друг от друга событий, следовательно, эффективная (суммарная) вероятность рассеивания равна:
(1)
где ![clip_image021[6]](/images/stories/clip_image0216_7a9e193bf8adfced30ee734b91759238.gif "clip_image021[6]"){kind=small}
— эффективное значение времени рассеяния, оно определяется из экспериментальных значений подвижности.
(2)
Умножим правую и левую части на 
.
(3)
(4)
где 
— эффективное значение подвижности, связанной со всеми типами центров рассеяния.
![clip_image221[1]](/images/stories/clip_image2211_0913e9511ace49bd218c848715be5e04.gif "clip_image221[1]"){kind=small}
— подвижность, связанная с рассеянием на k центре.
Рассмотрим пример. В атомарных полупроводниковых кристаллах с ковалентной связью (Ge, Si) основными механизмами рассеяния носителей заряда является рассеяние на ионах примеси (при низких температурах) и тепловых колебаниях решетки (при высоких температурах). Эффективное значение ![clip_image233[1]](/images/stories/clip_image233-1.gif "clip_image233[1]"){kind=small}
в этом случае должно определяться:
(5)
, 
, 
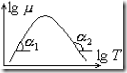Очевидно, при низких температурах 
При высоких температурах 
