Лекции для студентов

Электричество и магнетизм. Часть 1

1.9. Потенциалы простейших электрических полей.

Из соотношения , определяющего связь между напряженностью и потенциалом электрического поля, следует формула для вычисления потенциала поля:

где интегрирование производится вдоль силовой линии поля; С — произвольная постоянная, с точностью до которой определяется потенциал электрического поля.

Если направление поля совпадает с направлением радиус–вектора (), то вычисления можно производить по формуле:

.

Рассмотрим ряд примеров на применение этой формулы.

Пример1. Потенциал поля точечного заряда (рис.2.13).

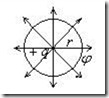
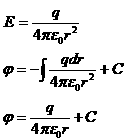
Рис.2.13. При полагают, что , тогда .

Таким образом, потенциал поля точечного заряда определяется по формуле:

Пример 2. Потенциал поля металлического заряженного шара.

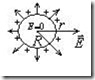а) Изолированный шар (рис.2.14).

при , т.е. внутри шара = const.

Рис2.14.

Вне шара .

При φ = 0, следовательно, С = 0.

 — вне шара.

Для определения используем свойство непрерывности потенциала: при переходе через границу поверхности шара, потенциал не претерпевает скачка. Полагая в последней формуле r =R, находим:

 — внутри шара.

б) Заземленный шар (рис.2.15).

.

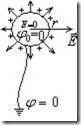
При , то есть  — вне шара.

Рис.2.15. Внутри шара φ(r ≤ 0) = φ₀ = 0.

Разность потенциалов U (рис.2.16) двух точек на силовой линии электрического поля заряженного шара определяется по формуле:

.

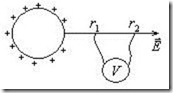
Рис.2.16.

Пример 3. Потенциал поля заряженной нити (рис.2.17).

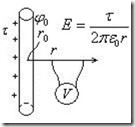При :

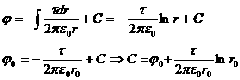
Рис.2.17.

Разность потенциалов U (рис.2.17) двух точек на силовой линии поля заряженной нити:

Пример 4. Потенциал поля заряженной плоскости (2.18).

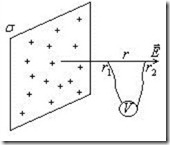
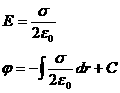
Рис.2.18.

Разность потенциалов U (рис.2.18) двух точек на силовой линии поля заряженной плоскости:

.