Лекции для студентов

Электричество и магнетизм. Часть 1

1.5. Применение теоремы Гаусса для расчета электрических полей.

В ряде случаев теорема Гаусса позволяет найти напряженность электрического поля протяженных заряженных тел, не прибегая к вычислению громоздких интегралов. Обычно это относится к телам, чья геометрическая форма обладает определенными элементами симметрии (шар, цилиндр, плоскость). Рассмотрим некоторые примеры применения теоремы Гаусса для расчета напряженности электрических полей.

Пример 1. Поле равномерно заряженной плоскости.

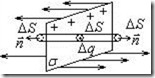Электрическое поле, создаваемое бесконечно протяженной равномерно заряженной плоскостью, является однородным — в каждой точке пространства вне плоскости его напряженность всюду одинакова. Направлено это поле перпендикулярно к плоскости в обе стороны (рис.2.5). Поэтому для потока вектора напряженности поля через произвольно выбранную цилиндрическую поверхность, опирающуюся на элемент плоскости ΔS, можем написать: , откуда 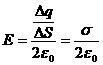, где — поверхностная плотность заряда. Размерность в СИ: .

Рис.2.5. Поле равномерно заряженной плоскости.

Таким образом, искомая напряженность электрического поля равномерно заряженной плоскости .

Пример 2. Поле равномерно заряженной нити (цилиндра).

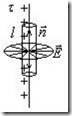В данном случае электрическое поле обладает аксиальной симметрией — не зависит от азимутального угла φ и координаты z и направлено вдоль радиус-вектора (рис.2.6). Поэтому для потока вектора через выбранную цилиндрическую поверхность с осью, совпадающей с заряженной нитью, имеем: , где  — элемент цилиндрической поверхности; l — длина произвольного участка нити.

С другой стороны, по теореме Гаусса этот поток равен: причем ,  — линейная плотность заряда нити.

Рис.2.6. Поле равномерно заряженной нити.

Отсюда находим: .

Искомая напряженность электрического поля равномерно заряженной нити:

.

Пример 3. Поле равномерно заряженного шара.

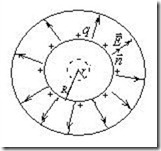а) Металлический шар. При равновесии заряды равномерно распределяются по внешней поверхности заряженного шара (рис.2.7). Поэтому при < (внутри шара) электрическое поле отсутствует: .

Рис.2.7. Поле равномерно заряженного металлического шара.

Вне шара (>) электрическое поле, созданное равномерно распределенными по его поверхности зарядами, обладает сферической симметрией (направлено по радиальным линиям), поэтому, согласно теореме Гаусса:

.

Видим, что электрическое поле равномерно заряженного металлического шара не зависит от радиуса шара и совпадает с полем точечного заряда.

б) Диэлектрический шар.

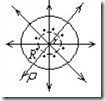Рассмотрим шар, с условной диэлектрической проницаемостью ε = 1, равномерно заряженный по объему с плотностью заряда (рис.2.8).

Размерность объемной плотности заряда в СИ: .

Рис.2.8. Поле равномерно заряженного диэлектрического шара.

Полный заряд шара, очевидно, есть: .

Имеем по теореме Гаусса:

1) Внутри шара (r < R): , где Δq = — заряд внутренней области шара, ограниченной выбранной сферической поверхностью радиуса r. Отсюда находим: .

2) Вне шара (r > R): , откуда = ,

то есть вне заряженного диэлектрического шара электрическое поле такое же, как и в случае металлического шара.

На рис.2.9 показан качественный ход зависимостей E(r) для металлического и диэлектрического шаров.

металл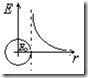 Рис.2.9. Зависимость E(r). 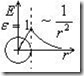диэлектрик