Электричество и магнетизм. Часть 1
- Электричество и магнетизм. Часть 1
- 1.2. Взаимодействие электрических зарядов. Закон Кулона
- 1.3. Электрическое поле. Напряженность электрического поля
- 1.4. Поток вектора напряженности электрического поля. Теорема Гаусса.
- 1.5. Применение теоремы Гаусса для расчета электрических полей.
- 1.6. Работа сил поля по перемещению заряда. Потенциал и разность потенциалов электрического поля.
- 1.7. Связь между напряженностью и потенциалом электрического поля. Градиент потенциала.
- 1.8. Эквипотенциальные линии и поверхности и их свойства.
- 1.9. Потенциалы простейших электрических полей.
- 1.10. Поляризация диэлектриков. Свободные и связанные заряды. Основные виды поляризации диэлектриков.
- 1.11. Вектор поляризации и вектор электрической индукции.
- 1.12. Напряженность электрического поля в диэлектрике.
- 1.13. Основные теоремы электростатики в интегральной и дифференциальной форме.
- 1.14. Граничные условия для электрического поля.
- 1.15. Равновесное распределение зарядов на проводниках.
- 1.16. Электроемкость проводников. Конденсаторы.
- 1.17. Вычисление емкости простых конденсаторов.
- 1.18. Соединение конденсаторов.
- 1.19. Энергия системы неподвижных точечных зарядов.
- 1.20. Энергия заряженного проводника и заряженного конденсатора.
- 1.21. Энергия электростатического поля.
Лекция 2
Основные уравнения электростатики в вакууме.
1.4. Поток вектора напряженности электрического поля. Теорема Гаусса.
По определению потоком векторного поля 
через площадку 
называется величина (рис.2.1)
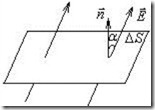
Рис.2.1. К определению потока вектора ![clip_image078[1]](/images/stories/clip_image0781_thumb_8ed4601b7c8c69d3ef54cabe54b488fa.gif "clip_image078[1]"){kind=small}
.
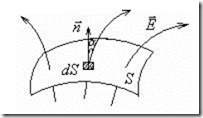
Если поле неоднородно или поверхность, через которую вычисляется поток, не является плоской (рис.2.2), то определение потока нужно применить к бесконечно малому элементу поверхности, а именно записать:
Тогда поток через всю поверхность S будет:
Рис.2.2. где 
.
Заметим, что поток — величина алгебраическая. Знак потока зависит от выбора направления нормали к элементарным площадкам, на которые разбивается поверхность S при вычислении ФЕ. Изменение направления нормали на противоположное изменит знак En, а значит и знак потока ФЕ. В случае замкнутых поверхностей принято считать знак потока положительным, если силовые линии поля выходят из охватываемой области наружу. Численно поток равен количеству силовых линий, пресекающих данную поверхность. Размерность потока в СИ: [ФЕ] = В·м (отметим, что она совпадает с размерностью величины q/εо).
Окружим точечный заряд q замкнутой сферической поверхностью радиуса r и вычислим поток электрического поля точечного заряда через эту поверхность (рис.2.3).
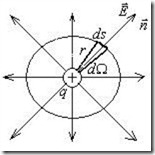По определению имеем: 
,
где 
— напряженность электрического поля в направлении внешней нормали, 
; 
— элемент поверхности, 
, 
— элемент телесного угла.
Рис.2.3. К доказательству теоремы Гаусса.
Вычисляем: 
Мы видим, что полученный результат не зависит от формы и размеров выбранной поверхности. Это очевидно, поскольку поток численно равен количеству силовых линий, пересекающих данную поверхность, и в случае выбора замкнутой поверхности любой другой формы он не изменится, так как силовые линии нигде не прерываются.
Если внутри замкнутой поверхности имеется несколько зарядов, то поток их результирующего поля, согласно принципу суперпозиции, будет равен:
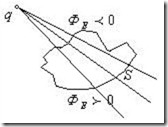
В частности, если система зарядов находится вне выбранной поверхности (рис.2.4) или алгебраическая сумма всех зарядов, заключенных под поверхностью, равна нулю, то поток 
.
Рис.2.4.
Доказанная выше теорема, носит название теоремы Гаусса (Gauss C., 1777–1855). Полная ее формулировка звучит так: поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности (деленной на 
):
Отметим, что теорема Гаусса является прямым следствием закона Кулона и является одной из основных теорем электростатики.
