Лекции для студентов

Электричество и магнетизм. Часть 1

1.11. Вектор поляризации и вектор электрической индукции.

Для количественной характеристики поляризации диэлектриков вводят понятие вектора поляризации как полного (суммарного) дипольного момента всех молекул в единице объема диэлектрика:

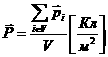,  — дипольный момент одной молекулы.

Суммирование производится по всем молекулам, находящимся в объеме V.

Легко видеть, что нормальная составляющая вектора поляризации Р_n численно равна поверхностной плотности поляризационных зарядов на диэлектрике σ ^′ (рис.3.10):

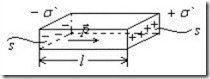
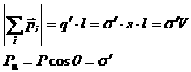
Рис.3.10. Вектор поляризации.

Последняя формула дает не только величину, но и знак поляризационных зарядов. В тех точках поверхности диэлектрика, где угол θ между внешней нормалью и вектором острый, σ ^′ положительна, а в тех точках, где угол между внешней нормалью и тупой, σ ^′ отрицательна.

Наряду с вектором поляризации , для описания электрического поля в диэлектриках вводят также понятие вектора электрической индукции . По определению:

где  — напряженность электрического поля в диэлектрике.

Для большинства диэлектриков (кроме сегнетоэлектриков) вектор поляризации

.

Безразмерная величина называется диэлектрической восприимчивостью. Она связана с поляризуемостью молекулы β данного диэлектрика простым соотношением: α = nβ, где n – число молекул в единице объема. В этом случае электрическая индукция

.

Постоянная называется диэлектрической проницаемостью (ε = 1 — для вакуума).

Таким образом, для многих изотропных диэлектриков можно считать, что