Электричество и магнетизм. Часть 1
- Электричество и магнетизм. Часть 1
- 1.2. Взаимодействие электрических зарядов. Закон Кулона
- 1.3. Электрическое поле. Напряженность электрического поля
- 1.4. Поток вектора напряженности электрического поля. Теорема Гаусса.
- 1.5. Применение теоремы Гаусса для расчета электрических полей.
- 1.6. Работа сил поля по перемещению заряда. Потенциал и разность потенциалов электрического поля.
- 1.7. Связь между напряженностью и потенциалом электрического поля. Градиент потенциала.
- 1.8. Эквипотенциальные линии и поверхности и их свойства.
- 1.9. Потенциалы простейших электрических полей.
- 1.10. Поляризация диэлектриков. Свободные и связанные заряды. Основные виды поляризации диэлектриков.
- 1.11. Вектор поляризации и вектор электрической индукции.
- 1.12. Напряженность электрического поля в диэлектрике.
- 1.13. Основные теоремы электростатики в интегральной и дифференциальной форме.
- 1.14. Граничные условия для электрического поля.
- 1.15. Равновесное распределение зарядов на проводниках.
- 1.16. Электроемкость проводников. Конденсаторы.
- 1.17. Вычисление емкости простых конденсаторов.
- 1.18. Соединение конденсаторов.
- 1.19. Энергия системы неподвижных точечных зарядов.
- 1.20. Энергия заряженного проводника и заряженного конденсатора.
- 1.21. Энергия электростатического поля.
1.2. Взаимодействие электрических зарядов. Закон Кулона. Применение закона Кулона для расчета сил взаимодействия протяженных заряженных тел.
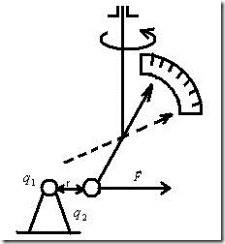
Закон взаимодействия электрических зарядов был установлен в 1785 г. Шарлем Кулоном (Coulomb Sh., 1736-1806). Кулон измерял силу взаимодействия двух небольших заряженных шариков в зависимости от величины зарядов и расстояния между ними с помощью специально сконструированных им крутильных весов (рис.1.3). В результате своих опытов Кулон установил, что сила взаимодействия двух точечных зарядов прямо пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними, при этом направление действия силы совпадает с прямой, проходящей через оба заряда:
~ 
, ![clip_image016[1]](/images/stories/clip_image0161_thumb_1556173c1a793095103a5e85032347ac.gif "clip_image016[1]"){kind=small}
~ 
, 
||
.
Другими словами, можем написать:
Коэффициент пропорциональности k зависит от выбора
единиц измерения входящих в эту формулу величин:
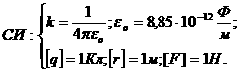
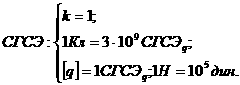Рис.1.3. Крутильные весы Кулона (схема).
В общепринятой сейчас Международной системе единиц измерения (СИ) закон Кулона записывается, следовательно, в виде:
Необходимо еще раз подчеркнуть, что в таком виде закон Кулона формулируется только для точечных зарядов, то есть таких заряженных тел, размерами которых можно пренебречь по сравнению с расстоянием между ними. Если это условие не выполняется, то закон Кулона должен быть записан в дифференциальной форме для каждой пары элементарных зарядов dq1 и dq2, на которые «разбиваются» заряженные тела:
.
Тогда полная сила взаимодействия двух макроскопических заряженных тел будет представлена в виде:
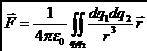
Интегрирование в этой формуле производится по всем зарядам каждого тела.
Пример. Найти силу F, действующую на точечный заряд Q со стороны бесконечно протяженной прямолинейной заряженной нити (рис.1.4). Расстояние от заряда до нити a, линейная плотность заряда нити τ.
Рис.1.4. К расчету силы F.
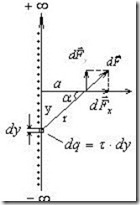
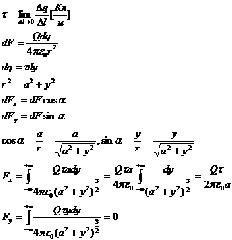
Искомая сила F = Fx= Qτ/(2πε0a).
