Электричество и магнетизм. Часть 1
- Электричество и магнетизм. Часть 1
- 1.2. Взаимодействие электрических зарядов. Закон Кулона
- 1.3. Электрическое поле. Напряженность электрического поля
- 1.4. Поток вектора напряженности электрического поля. Теорема Гаусса.
- 1.5. Применение теоремы Гаусса для расчета электрических полей.
- 1.6. Работа сил поля по перемещению заряда. Потенциал и разность потенциалов электрического поля.
- 1.7. Связь между напряженностью и потенциалом электрического поля. Градиент потенциала.
- 1.8. Эквипотенциальные линии и поверхности и их свойства.
- 1.9. Потенциалы простейших электрических полей.
- 1.10. Поляризация диэлектриков. Свободные и связанные заряды. Основные виды поляризации диэлектриков.
- 1.11. Вектор поляризации и вектор электрической индукции.
- 1.12. Напряженность электрического поля в диэлектрике.
- 1.13. Основные теоремы электростатики в интегральной и дифференциальной форме.
- 1.14. Граничные условия для электрического поля.
- 1.15. Равновесное распределение зарядов на проводниках.
- 1.16. Электроемкость проводников. Конденсаторы.
- 1.17. Вычисление емкости простых конденсаторов.
- 1.18. Соединение конденсаторов.
- 1.19. Энергия системы неподвижных точечных зарядов.
- 1.20. Энергия заряженного проводника и заряженного конденсатора.
- 1.21. Энергия электростатического поля.
1.6. Работа сил поля по перемещению заряда. Потенциал и разность потенциалов электрического поля.
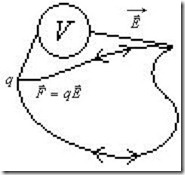 Как следует из закона Кулона, сила, действующая на точечный заряд q в электрическом поле, созданном другими зарядами, является центральной. Напомним, что центральной называется сила, линия действия которой направлена по радиус-вектору, соединяющему некоторую неподвижную точку О (центр поля) с любой точкой траектории. Из «Механики» известно, что все центральные силы являются потенциальными. Работа этих сил не зависит от формы пути перемещения тела, на которое они действуют, и равна нулю по любому замкнутому контуру (пути перемещения). В применении к электростатическому полю (рис.2.10):
Как следует из закона Кулона, сила, действующая на точечный заряд q в электрическом поле, созданном другими зарядами, является центральной. Напомним, что центральной называется сила, линия действия которой направлена по радиус-вектору, соединяющему некоторую неподвижную точку О (центр поля) с любой точкой траектории. Из «Механики» известно, что все центральные силы являются потенциальными. Работа этих сил не зависит от формы пути перемещения тела, на которое они действуют, и равна нулю по любому замкнутому контуру (пути перемещения). В применении к электростатическому полю (рис.2.10):
![]() .
.
Рис.2.10. К определению работы сил электростатического поля.
То есть, работа сил поля по перемещению заряда q из точки 1 в точку 2 равна по величине и противоположна по знаку работе по перемещению заряда из точки 2 в точку 1, независимо формы пути перемещения. Следовательно, работа сил поля по перемещению заряда может быть представлена разностью потенциальных энергий заряда в начальной и конечной точках пути перемещения:
![]() .
.
Введем потенциал электростатического поля φ, задав его как отношение:
![]()
![]() , (размерность в СИ:
, (размерность в СИ: ![]() ).
).
Тогда работа сил поля по перемещению точечного заряда q из точки 1 в точку 2 будет:
![]()
Разность потенциалов ![]() называется электрическим напряжением. Размерность напряжения, как и потенциала, [U] = B.
называется электрическим напряжением. Размерность напряжения, как и потенциала, [U] = B.
Считается, что на бесконечности электрические поля отсутствуют, и значит![]() . Это позволяет дать определение потенциала как работы, которую нужно совершить, чтобы переместить заряд q = +1 из бесконечности в данную точку пространства. Таким образом, потенциал электрического поля является его энергетической характеристикой
. Это позволяет дать определение потенциала как работы, которую нужно совершить, чтобы переместить заряд q = +1 из бесконечности в данную точку пространства. Таким образом, потенциал электрического поля является его энергетической характеристикой
