Электричество и магнетизм. Часть 1
- Электричество и магнетизм. Часть 1
- 1.2. Взаимодействие электрических зарядов. Закон Кулона
- 1.3. Электрическое поле. Напряженность электрического поля
- 1.4. Поток вектора напряженности электрического поля. Теорема Гаусса.
- 1.5. Применение теоремы Гаусса для расчета электрических полей.
- 1.6. Работа сил поля по перемещению заряда. Потенциал и разность потенциалов электрического поля.
- 1.7. Связь между напряженностью и потенциалом электрического поля. Градиент потенциала.
- 1.8. Эквипотенциальные линии и поверхности и их свойства.
- 1.9. Потенциалы простейших электрических полей.
- 1.10. Поляризация диэлектриков. Свободные и связанные заряды. Основные виды поляризации диэлектриков.
- 1.11. Вектор поляризации и вектор электрической индукции.
- 1.12. Напряженность электрического поля в диэлектрике.
- 1.13. Основные теоремы электростатики в интегральной и дифференциальной форме.
- 1.14. Граничные условия для электрического поля.
- 1.15. Равновесное распределение зарядов на проводниках.
- 1.16. Электроемкость проводников. Конденсаторы.
- 1.17. Вычисление емкости простых конденсаторов.
- 1.18. Соединение конденсаторов.
- 1.19. Энергия системы неподвижных точечных зарядов.
- 1.20. Энергия заряженного проводника и заряженного конденсатора.
- 1.21. Энергия электростатического поля.
1.19. Энергия системы неподвижных точечных зарядов.
Как мы уже знаем, силы с которыми взаимодействуют заряженные тела, являются потенциальными. Следовательно, система заряженных тел обладает потенциальной энергией. Когда заряды удалены друг от друга на бесконечность, они не взаимодействуют. Положим в этом случае их энергию равной нулю.
Рис.4.9. К определению энергии системы зарядов.
Рассмотрим сначала систему, состоящую из двух точечных зарядов (рис.4.9). Cблизим заряды на заданное расстояние r. При этом мы совершим работу против сил электрического поля, которая пойдет на увеличение потенциальной энергии системы. Сближение зарядов можно произвести, приближая q2 к q1 либо q1 к q2. В обоих случаях совершается одинаковая работа:
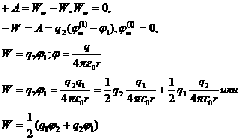
В последней формуле 
— потенциал поля 1-го заряда в том месте, где находится второй заряд; 
— потенциал поля второго заряда в том месте, где находится первый заряд. С учетом сказанного, эту формулу можно записать также в виде:
.
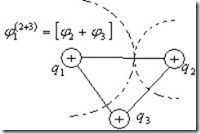
Рис.4.10. Система трех неподвижных точечных зарядов.
Нетрудно убедиться в том, что потенциальная энергия системы трех неподвижных точечных зарядов (рис.4.10) может быть представлена в виде:
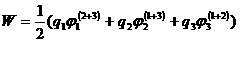
В общем случае системы n неподвижных точечных зарядов энергия системы определяется по формуле:
