Лекции для студентов

Электричество и магнетизм. Часть 1

Напряженность и потенциал — это две характеристики одного и того же объекта — электрического поля, поэтому между ними должна существовать функциональная связь. Действительно, работа сил поля по перемещению заряда q из одной точки пространства в другую может быть представлена двояким образом:

Откуда следует, что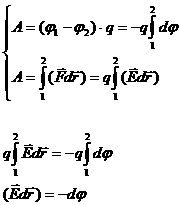

Или

Это и есть искомая связь между напряженностью и потенциалом электрического поля в дифференциальном виде.

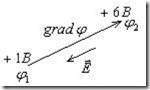
 — вектор, направленный из точки с меньшим потенциалом в точку с большим потенциалом (рис.2.11).

, .

Рис.2.11. Векторыи gradφ. .

Из свойства потенциальности электростатического поля следует, что работа сил поля по замкнутому контуру (φ₁= φ₂) равна нулю:

,

поэтому можем написать

Последнее равенство отражает суть второй основной теоремы электростатики — теоремы о циркуляции электрического поля, согласно которой циркуляция поля вдоль произвольного замкнутого контура равна нулю. Эта теорема является прямым следствием потенциальности электростатического поля.