Лекция по системному анализу в чрезвычайных ситуациях. Часть 3
- Лекция по системному анализу в чрезвычайных ситуациях. Часть 3
- 2.1.2. Характеристики техносферной системы
- 2.1.3. Особенности организации и динамики систем
- 2.1.4. Энергоэнтропийная концепция опасностей
- 2.1.5. Показатели качества обеспечения безопасности техносферы
- 2.1.6. Формализация и моделирование безопасности.
- 2.1. Место математического моделирования в системных исследованиях
- 2.2. Типы и виды математических моделей
- 2.3. Процесс построения математической модели
- Этап 1. Содержательная постановка
- Этап 2. Концептуальная постановка
- Этап 3. Качественный анализ
- Этап 4. Построение математической модели
- Этап 5. Разработка компьютерных программ
- Этап 6. Анализ и интерпретация результатов моделирования
- 2.4. Структура моделирования происшествий в техносфере
- Тема 2.2.2 Часть 1: Моделирование на основе теории катастроф
- Тема 2.2.2 Часть 2: Установление связи между показателями. Регрессионный анализ.
- Тема 2.2.3: Формальная записаь и общие свойства
- Общие свойства
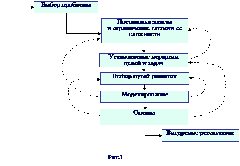
Из рассмотренного ранее нам должно быть понятно, что системный анализ не есть какой-то конкретный метод. Это стратегия научного поиска, которая использует математические концепции, математический аппарат в рамках систематизированного научного подхода к решению сложных проблем. При этом так или иначе выделяется ряд последовательных, взаимосвязанных этапов (рис. 1).Рассмотрение вместо самой системы (т.е. явления, процесса, объекта) и модели всегда связано с упрощением. Главная проблема здесь — выделение тех особенностей, которые существенны для целей рассмотрения. К настоящему времени разработано множество удачных моделей, например, такие как:
- конечноэлементная модель для решения различных прикладных задач (статика, динамика, прочность конструкций, динамика оболочек и т.п.);
- генетический код;
и др.
Ранее нами было выделено два основных вида моделей: материальные (макеты, физические модели, масштабированные модели и т.п.) и идеальные (вербальные, знаковые).
При построении моделей процессов в техносфере приходится прибегать как к так называемым интуитивным («ненаучным») моделям, так и к семантическим (смысловым).
Под интуитивным моделированием подразумевают моделирование, использующее представление объекта, не обоснованное с точки зрения формальной логики. Это представление может не поддаваться, или трудно поддаваться формализации или же вообще не нуждаться в ней. Такое моделирование человек осуществляет в своем сознании в форме мысленных экспериментов, сценариев и игровых ситуаций с целью подготовки к предстоящим практическим действиям. Основой для подобных моделей служит опыт — знания и умения людей, а также любое эмпирическое знание, полученное из эксперимента или процесса наблюдения без объяснения причин и механизма наблюдаемого явления.
Семантическое моделирование, в отличие от интуитивного, логически обосновано с помощью некоторого числа исходных предположений. Сами эти предположения нередко облекаются в форму гипотез. Семантическое моделирование предполагает знание внутренних механизмов явления. К методам семантического моделирования относятся вербальное (словесное) и графическое моделирование (см. рис. 2).
Семиотическое, или знаковое моделирование является, в отличие от семантического, наиболее формализованным, поскольку использует не только слова естественного языка и изображения, но и различные символы — буквы, цифры, иероглифы, нотные знаки. В последующем все они объединяются с помощью специфических правил. К этому виду моделирования относится математическое моделирование.
К знаковым моделям относятся химические и ядерные формулы, графики, схемы, графы, чертежи, топографические карты и т.п. Среди знаковых моделей выделяется их высший класс — математические модели, т.е. модели, при описании которых используется язык математики.
Математическая модель (ММ) — это описание протекания процесса, описание состояния или изменения состояния системы на языке алгоритмических действий с математическими формулами и логических переходов.
Кроме того, ММ допускает работы с таблицами, графиками, номограммами, выбор из совокупности процедур и элементов (последнее подразумевает использование операций предпочтения, частичной упорядоченности, включения, определение принадлежности и т.п.).
Различные математические правила манипулирования со связями системы позволяют делать предсказания относительно тех изменений, которые могут произойти в исследуемых системах, когда изменяются их составляющие.
Сложность формирования математической модели связана с необходимостью владения математическими методами и предметных знаний, т.е. знаний в той области, для которой создается модель. В реальности специалисту в данной практической области часто не хватает математических знаний, сведений о моделировании вообще, а для сложных задач — знания системного анализа. С другой стороны, прикладному математику трудно хорошо ориентироваться в предметной области.
Следует заметить, что деление моделей на вербальные, натурно знаковые в определенной степени условно. Так, существуют смешанные типы моделей, скажем, использующие и вербальные, и знаковые построения. Можно даже утверждать, что нет знаковой модели без сопровождающей описательной — ведь любые знаки и символы необходимо пояснять словами. Часто и отнесение модели к какому-либо типу является нетривиальным.
Общие и конкретные модели. Все типы моделей необходимо перед их применением к конкретной системе наполнить информацией, соответствующей используемым силам, макетам, общим понятиям. Наполнение информацией в большей степени свойственно знаковым моделям, в наименьшей — натурным. Так, для математической модели — это выделенные (вместо буквенных) значения физических величин коэффициентов, параметров; конкретные виды функций, определенные последовательности действий, графы структуры Наполненную информацией модель принято называть конкретной, содержательной.
Модель без наполнения информацией до уровня соответствия единичной реальной системе называется общей (теоретически абстрактной, системной).
Так, в процессе декомпозиции мы используем понятие формальной модели. Это относится ко всем типам моделей, в том числе, к математическим.
Чтобы уяснить место математической модели рассмотрим процесс формирования собственно научного знания. Принято делить науки на две группы.
а) точные — (скорее термин «точные» основан на вере, что открываемые закономерности являются абсолютно точными);
б) описательные.
Точные науки — обладают средствами предвидеть с практически достаточной точностью развитие процессов, изучаемых данной наукой на достаточно длительный (опять-таки по практическим соображениям) промежуток времени, или же предвидеть достаточно точно свойства и отношения изучаемых объектов по некоторой частичной информации о них.
Описательные науки – по сути перечень фактов об изучаемых ими объектах и процессах, иногда не связанных между собой, иногда связанных некоторыми качественными отношениями, а также порой разрозненными количественными (как правило, эмпирическими связями). К точным наукам относятся математика и науки физического цикла. Остальные науки — в большей или меньшей степени являются описательными.
Однако в Древнем Египте даже математика не могла быть в полной мере отнесена к точным наукам (так, геометрия была представлена как «сборник рецептов», например, вычислять площадь круга как ¾ площади описанного квадрата).
Развитие науки идет параллельными путями («руслами»). Различные русла начинаются в разное время, но раз начавшись, продолжаются.
1) накопление информации об объектах изучения; (научное накопление информации отличается от стихийного целеустремленностью);
2) процесс упорядочивания информации — классификация объектов (отличие от «наивной», «потребительской» классификации — цель: обеспечить анализ, следовательно субъективизма меньше) → находятся в постоянной взаимосвязи (процесс идентификации), т.е. каждый новый объект анализируется: принадлежит ли он к уже установленным классификационным группам, или указывает на необходимость перестройки системы классификации;
3) установление связей и соотношений (качественных или количественных) между объектами. Эти связи обнаруживаются в результате постоянного анализа накапливаемой и упорядоченной информации.
Эти три русла характеризуют «описательный» период развития науки, который может длиться весьма долго. Примером может служить развитие механики, геометрии.
Переход к точной науке означает попытки построения математического моделирования процессов. Но математическая модель может строиться на каких-то количественно строго определенных величинах. Отсюда — два необходимых этапа математического моделирования:
4) установление величины;
5) установление взаимосвязи.
![clip_image003[4] clip_image003[4]](/images/stories/clip_image0034_thumb_be12fc00c84e8b11e12ab1070697a43f.gif) ![clip_image004[4] clip_image004[4]](/images/stories/clip_image0044_thumb_9af6e8220f93e694cd73b28304d638a3.gif)  ![clip_image006[4] clip_image006[4]](/images/stories/clip_image0064_thumb_c4bf363dd6baeb931b0d270ebc0ac06a.gif)     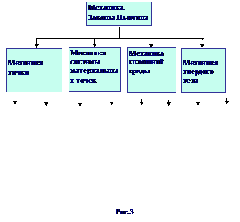 |
Можно привести следующий пример: законы статики сформулировал Архимед, Аристотель ввел понятие силы, скорости, пути. Но потребовалось около 2000 лет (!) на установление связи величин. Становление механики как точной науки стало возможным, когда Ньютон понял, что силу надо связывать с ускорением, а не скоростью, как это пытались делать раньше.
Задачи математического моделирования сами имеют свою сложную структуру. Модель, описывающая широкий класс явлений (например, математическая модель механических движений — законы Ньютона) подразделяются на частные классы математических моделей: механика точки, системы материальных точек, сплошной среды, твердого тела → еще более частные модели, например, упругого тела и т.п. на самом нижнем уровне — ММ конкретных процессов.
Обычно процесс построения моделей часто осуществляется не дедуктивно, а «снизу вверх».
![clip_image002[4] clip_image002[4]](/images/stories/clip_image0024_thumb_069602ccbd937692a7d967f6bcf90240.gif)
