Лекции для студентов

Лекция по системному анализу в чрезвычайных ситуациях. Часть 3

2.1.3. Особенности организации и динамики систем

Вспомним, что одной из важнейших характеристик системы является ее состояние как совокупность всех ее существенных свойств на момент проявления. Функционирование системы есть процесс смены состояний при неизменности в времени и пространстве обобщенной структуры системы. Развитие системы подразумевает изменение, перестройку структуры системы.

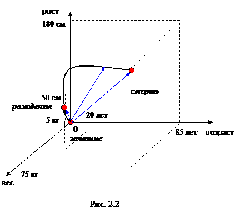
Сам процесс функционирования или развития системы может быть представлен как ее перемещение по некоторой траектории. В свою очередь, каждая точка такой траектории может быть интерпретирована в виде вектора соответствующих интегральных переменных (показателей) системы. Сама же траектория принадлежит пространству всех ее возможных состояний, характеризуемому размерностью не меньшей, чем число тех показателей, которые входят в только что обозначенный вектор. Примером может служить физический цикл существования организма, например, человеческого (см. рис. 2.2), где в качестве показателей взяты возраст, вес и рост.

Каждый год, прожитый человеком или человеко-машинной системой, будет отличаться хотя бы одним из соответствующих показателей-координат, т.е. иметь определенное положение в выбранном пространстве состояний. Линия, соединяющая все соответствующие его точки — концы векторов, или годограф, и есть траектория системы. Траекторию системы для наглядности можно проецировать на какую-либо плоскость пространства состояний.

Что касается динамики техносферы и человеко-машинных систем, то здесь следует отметить следующие обстоятельства:

1) число возможных состояний таких систем ограничено,

2) выбор таких состояний не может быть произвольным.

Это объясняется тем, что такие системы обладают естественным стремлением к устойчивости, стабильности и живучести. При этом каждому диапазону внешних воздействий соответствует лишь одно, вполне определенное состояние системы. Поскольку общий диапазон подобных воздействий ограничен, общее количество состояний системы конечно.

Процесс функционирования системы обусловлен строго определенными соотношениями между энергией внешнего возмущения и собственной энергоемкостью конкретного ее состояния. Если внешняя энергия не превышает некоторых пороговых значений, не накапливается в системе, а уменьшается в результате частичного рассеивания или преобразования в другую энергию, то реакция системы на данное возмущение проявляется лишь в незначительном колебании своих существенных показателей, либо в их эволюционном изменении.

Один из наиболее общих механизмов сохранения системой стабильности связан с т.н. принципом Ле-Шателье — Брауна, в соответствии с которым любое внешнее воздействие порождает ответную реакцию системы, направленную на ослабление его эффекта и сохранения гомеостазиса. Нахождение таких систем в устойчивом или стабильном 0состоянии проявляется в относительной неизменности их обобщенной структуры и интегральных показателей.

Смена или утрата определенных состояний системы иногда сопровождается структурной перестройкой и происходит скачкообразно. Нередко это связано с причинением системе некоторого ущерба. Это связано с тем, что компенсационные механизмы системы уже не способы удержать ее в прежнем состоянии, и она утрачивает стабильность из-за радикальной перестройки своей структуры и скачкообразного изменения интегральных показателей.

Выбор направления смены состояний осуществляется, как правило, ради сохранения системой своей устойчивости и стабильности, причем из ограниченного числа альтернатив. Чаще всего необходимость выбора альтернативного состояния возникает при выходе системы на так называемый «режим с обострением», который может завершаться кризисами и катастрофами.

Кризис следует расценивать как свидетельство необходимости обновления, улучшения системы.

Катастрофа, в отличие от кризиса, сопровождается значительным и резким изменением интегральных показателей системы вследствие коренной перестройки структуры и морфологии.

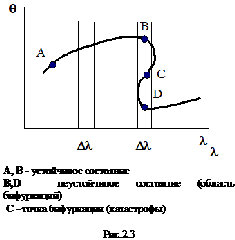Под катастрофой в математике понимается скачкообразное изменение состояния системы при малом изменении управляющих параметров. Такое изменение бывает возможно далеко не всегда, и лишь тогда, когда система находится в неустойчивом состоянии (состояние неустойчивого равновесия). Например, мы повернули руль совсем чуть-чуть не вправо, а влево, и автомобиль оказался в кювете; оператор АЭС совсем немного выдвинул стержни, и реактор начал разогреваться в аварийном режиме. С катастрофой в математике связан также термин "бифуркация".

Бифуркация — означает «раздвоение». Этот термин употребляют в широком смысле для обозначения всевозможных качественных перестроек и метаморфозу различных параметров, от которых они зависят.

Иногда выделяют понятие катаклизма как чрезвычайно сильные изменения, появление которых равносильно краху, т.е. прекращению существования системы.

Функционирование техносферной системы характеризуется, таким образом, следующими возможными ситуациями:

1) гомеостазис (динамическое равновесие),

2) различные возмущенные состояния, вызванные ошибками людей (человеческий фактор), отказами техники, неблагоприятными внешними воздействиями,

3) опасные, критические и катастрофические состояния.

Таким образом, можно сформулировать основные положения динамики сложной системы.

1. Поведение системы является следствие взаимодействия наиболее существенных ее элементов между собой и с окружающей средой.

2. Определяющее влияние на поведение системы оказывают те звенья ее морфологии, которые включают в себя обратные связи.

Из этих положений следует, что поведение любой системы зависит не только от характера каких-либо воздействий на нее, но и, в значительной, а иногда и в определяющей степени от самой системы.

3. Проблемы создаются преимущественно внутри системы, а не в ее окружении.

Из этого следует, что поиск причин возникающих проблем следует искать прежде всего в самой системе.

4. Изучить сложную систему означает установить наиболее существенные отношения между ее элементами и окружающей их средой.

5. При исследовании сложной системы важно понять ее структуру, прежде чем количественно оценить и спрогнозировать все ее существенные характеристики.

6. Конечная цель изучения сложной системы — это анализ эффективности различных путей усовершенствования, улучшения системы.

Из трех последних положений следует, что количественный анализ любых сложных систем чрезвычайно трудоемок, поскольку надо не только выявить их состав, структуру, морфологию и функциональную среду, но и определиться с параметрами, показателями и интегральными характеристиками как всей системы, так и ее существенных компонентов.

Что касается техносферы в целом и различных человеко-машинных систем, то их особенности, существенные для моделирования и прогнозирования заключаются в следующем. Во-первых, это трудоемкость моделирования и системного анализа человеко-машинной системы, во-вторых, невозможность точного прогноза интегральных показателей столь сложной системы, не говоря уже о траектории ее изменения. Это требует привлечения методов математической статистики и теории нечетких множеств. Основатель теории нечетких множеств Л. Заде сформулировал так называемый принцип несовместности: чем сложнее система, тем менее правдоподобны точные количественные предсказания ее будущего поведения; если же сложность системы превосходит некоторый пороговый уровень, то точность количественного прогноза и практический смысл становятся почти исключающими друг друга характеристиками.

Таким образом, для повышения результативности системного исследования техносферы, моделирования безопасности, чрезвычайных ситуаций, необходимо основное внимание уделять уяснению тех внутренних закономерностей и узких мест, воздействие на которые окажется наиболее результативным.