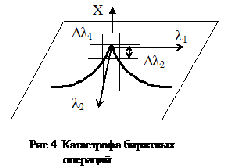Лекции для студентов

Лекция по системному анализу в чрезвычайных ситуациях. Часть 3

Тема 2.2.2 Часть 1: Моделирование на основе теории катастроф

Под катастрофой в математике понимается скачкообразное изменение состояния системы при малом изменении управляющих параметров. Такое изменение бывает возможно далеко не всегда, и лишь тогда, когда система находится в неустойчивом состоянии (состояние неустойчивого равновесия). Например, мы повернули руль совсем чуть-чуть не вправо, а влево, и автомобиль оказался в кювете; оператор АЭС совсем немного выдвинул стержни, и реактор начал разогреваться в аварийном режиме. С катастрофой в математике связан также термин "бифуркация".

Бифуркация — означает «раздвоение». Этот термин употребляют в широком смысле для обозначения всевозможных качественных перестроек и метаморфозу различных параметров, от которых они зависят.

Важную роль в создании теории катастроф сыграли работы Р. Тома («Структурная устойчивость и морфогенез»), в которой он рассматривал проблемы морфогенеза с точки зрения прикладной математики. Речь идет о выделении наиболее существенных особенностей на начальных стадиях развития организма и их математическом описании. Наиболее важным в морфогенезе является появление новых качеств, например, изменения типа симметрии, наблюдаемые в ходе развития организма.

Характерной чертой биологических и многих других систем (технических, социальных) являются скачки — внезапные перестройки, происходящие при непрерывном варьировании параметров. Эти внезапные изменения были названы Р. Тома катастрофами.

В динамике систем иногда возникают ситуации, когда при плавном изменении параметра l в критической точке происходит скачок. Пример — см. рис. 2, когда скачком появляется или исчезает мера состояний равновесия.

В технике с этой биофуркацией часто связан эффект «хлопка» или «прощелкивания».

В ряде случаев они являются причинами аварий.

При исследовании динамики большой системы, когда цель не является четко обозначенной, часто делается попытка минимизации некоторой функции полезности (функции цены).

Пусть, например, l₁, l₂ …l_k — параметры управления большой системы. Они принимают значения х₁^*, х₂^*, х^*_n в состоянии равновесия, при котором достигается локальный минимум функций f(x₁ , x₂ … x_n , l₁,l₂… l_к). Значение х_i^* зависят от выбора параметров a, т.е.

х_i^* = х_i^* (l), I = 1, n. .В этом случае катастрофа — это скачкообразные изменения параметров х, происходящие в результате плавного изменения параметров А.

Теория катастроф позволила провести классификацию «типичных» критических точек и выяснить, какими бывают «типичные катастрофы» при различном числе параметров l, определяющих состояние системы («катастрофы» сборки…).

Пример. Рассматриваются биржевые операции (Состояние системы описывается скоростью изменения индекса Доу-Джонса на бирже).

Входные переменные:

l₁ — дополнительный спрос на акции со стороны покупателей;

l₂ — доля денежных средств, направленная на спекулятивные операции.

Для моделирования функционирования биржи предлагается использовать уравнение типа сборки

Используется тот факт, что вдоль линий сборки

.

и определяется связь между l₁ и l₂, а затем минимальные изменения Dl₁ и Dl₂ для пересечения бифуркационной кривой..

В частности, для модели биржевых операций было получено Dl₁>Dl₂, т.е. модель биржевых операций обладает более высокой адаптивностью (~ в 2 раза) по отношению к изменению спроса на акции со стороны покупателей, чем к изменению средств, направленных на спекулятивные операции.

Ограничения к применению математического аппарата теории катастроф:

1) динамика большой системы описывается гладкой функцией;

2) вектор параметров системы имеет не больше пяти компонентов;

3) большая система рассматривается как «черный ящик».

Таким образом, математический инструментарий весьма ограничен, несмотря на большую философскую привлекательность теории катастроф.