Лекция по системному анализу в чрезвычайных ситуациях. Часть 3
- Лекция по системному анализу в чрезвычайных ситуациях. Часть 3
- 2.1.2. Характеристики техносферной системы
- 2.1.3. Особенности организации и динамики систем
- 2.1.4. Энергоэнтропийная концепция опасностей
- 2.1.5. Показатели качества обеспечения безопасности техносферы
- 2.1.6. Формализация и моделирование безопасности.
- 2.1. Место математического моделирования в системных исследованиях
- 2.2. Типы и виды математических моделей
- 2.3. Процесс построения математической модели
- Этап 1. Содержательная постановка
- Этап 2. Концептуальная постановка
- Этап 3. Качественный анализ
- Этап 4. Построение математической модели
- Этап 5. Разработка компьютерных программ
- Этап 6. Анализ и интерпретация результатов моделирования
- 2.4. Структура моделирования происшествий в техносфере
- Тема 2.2.2 Часть 1: Моделирование на основе теории катастроф
- Тема 2.2.2 Часть 2: Установление связи между показателями. Регрессионный анализ.
- Тема 2.2.3: Формальная записаь и общие свойства
- Общие свойства
1. Функция регрессии
2. Линейная регрессия
Если функциональная зависимость между двумя показателями неизвестна, обычно пытаются установить тесноту их связи, измерить степень их зависимости. При этом прибегают к методам корреляционно-регресионного анализа.
Пусть х — независимая переменная, у — зависимая переменная.
Зависимость х от у называется функциональной, если каждому значению х соответствует единственное значение у (при этом и х и у могут быть как детерминированными, так и случайными).
Если каждому фиксированному значению х соответствует множество у, мы имеем стохастическую зависимость. Среднее значение (групповое генеральное среднее) этого множества (при х = х) называется математическим ожиданием случайной величины у, вычисленным при условии, что х = х.
Таким образом, необходимо выяснить, изменяются или нет при изменении х условные математические ожидания М(У/Х=х). Если изменяются, то имеет место корреляционная зависимость у от х, если нет, то отсутствует.
Функция регрессии. Функция f(x) = M(У/Х=х), описывающая изменение условного математического ожидания случайной переменной У при изменении значений х переменной Х, называется функцией регресии.
Обычно используют коэффициент парной корреляции или генеральное корреляционное отношение, который может изменяться от 0 до 1 или от –1 до 1 (коэффициент парной корреляции).
Коэффициент корреляции может отличаться от 0 в следующих случаях:
1) У причинно зависит от Х;
2) Х причинно зависит от У;
3) У и Х непосредственно не влияют друг на друга, но совместно зависят от одного или нескольких факторов, причинно влияющих на Х и У;
4) Имеет место простое совпадение согласованности изменений х и у.
 |
Само по себе установление причинно-следственных связей является важной задачей. Используются различные способы формирования связей между внешними факторами и показателями системы. Например, может быть использован экспертный метод с привлечением коллективов экспертов разных специальностей.
2. Линейная регрессия
Модели, которые состоят из линейной комбинации определенного набора функций Xk называются, линейными моделями, и для минимизации разности между моделью и данными может использоваться линейная регрессия. Общая форма модели этого вида
где Xk (x) — функции x, которые называются, функциями базиса, и ak — свободные параметры. Заметьте, что слово "линейный" относится только к зависимости модели от параметров ak; функции Xk (x) могут быть нелинейны.
Минимизация линейной модели выполнется относительно оценочной функции
Минимум этого выражения достигается при равенстве нулю его производной по параметрам. Заменив линейную модель этой функцией, возьмем первые производные и приравняем их к нулю. В результате получим уравнения, которые могут быть решены относительно параметров ak.
Модели линейной регрессии могут быть следующими:
· линейной Y = a+bx
· квадратичной Y = a+bx+cx2
· полиномиальной: Y = a+bx+cx2+dx3 + ....
Обычно при исследовании реальной системы мы имеем набор данных (точек), часто называемых "наблюдениями". Задача состоит в том, чтобы связать эти данные, построив модель в форме параметрического уравнения. Это "модельное уравнение " может, в зависимости от желания исследователя и особенностей конкретной системы, представлять собой различные функции: от простого полинома до чрезвычайно сложной модели с многими параметрами. Желательно, чтобы модель была выбрана так, чтобы параметры в выражении имели реальные интерпретацию и значения.
Моделирование данных может выполняться несколькими методами: интерполяция, регрессия, или сглаживание данных. Интерполяция гарантирует, что аппроксимирующая кривая пройдет через каждую точку. Регрессия просто гарантирует, что "оценочная функция", т.е. некоторая произвольная функция, которая измеряет несоответствие между данными и моделью будет минимизирована. При этом подходе, параметры модели подбираются до тех пор, пока оценочная функция не достигнет минимума.
Стандартная ошибка и коэффициент корреляции. При подборе функции регрессии, погрешность оценивается с помощью стандартной ошибки и коэффициента корреляции. Эти инструментальные средства не совершенны, но они дают полезную оценку деятельности посадки кривой. Стандартная ошибка определена следующим образом:
где f(xi) - значения, рассчитанные по модели регрессии, yi - точки данных, и n — число параметров в конкретной модели (так, чтобы знаменатель соответствовал числу степеней свободы). Стандартная ошибка определяет разброс точек данных вокруг кривой регрессии. По мере улучшения качества модели стандартная ошибка приближается к нулю.
Другой критерий "согласия" — это коэффициент корреляции. Чтобы объяснить значение этого критерия, мы должны возвратиться точкам данных и определить допустимое отклонение, которое определяет величину разброса данных вокруг среднего:
Где среднее число точек данных y задается как
Величина St рассматривает разброс вокруг постоянной линии (среднее) в отличие от разброса вокруг модели регрессии. Это — неопределенность зависимой переменной от регрессии. Мы также определяем отклонение от сглаживающей кривой как
Это выражение по форме напоминает формулу для стандартной ошибки, приведенной выше; Оно дает нам разброс точек вокруг подобранной функции. Таким образом, уменьшение погрешности может быть определено количественно как разность этих двух чисел. Поскольку эта величина зависит от масштаба данных, разность отнесена к значению St (нормирована).
где r — коэффициент корреляции. Когда регрессионная зависимость хорошо описывает данные, коэффициент корреляции близок к единице, а стандартная ошибка близка к нулю.
![clip_image002[8] clip_image002[8]](/images/stories/clip_image0028_thumb_074f8429627d92cecdfb0a95ba4bb209.gif)
![clip_image008[6] clip_image008[6]](/images/stories/clip_image008-6_thumb.gif)
![clip_image010[6] clip_image010[6]](/images/stories/clip_image010-6_thumb.gif)
![clip_image012[4] clip_image012[4]](/images/stories/clip_image012-4_thumb.gif)
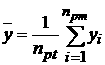
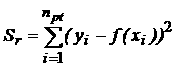
![clip_image018[4] clip_image018[4]](/images/stories/clip_image0184_thumb_372a9b36345e8c042fa3ddd7962938c5.gif)
