Лекция по “Теории полёта”. Часть 2
- Лекция по “Теории полёта”. Часть 2
- Метод последовательных приближений
- Рассмотрим выполнение программного угла Θ
- Интеграл момента количества движения
- Интеграл энергии
- Уравнение траектории пассивного участка
- Уравнение эллиптического участка траектории
- Время полета ракеты на эллиптической траектории
- Расчет участка снижения
- Определение оптимального угла траектории
- Орбитальные движения тел . Законы Кеплера .
- Вывод искусственного спутника Земли (ИСЗ) на орбиту
- Кинематические уравнения , связанные с движением ИСЗ
- Траектория полета космических кораблей
- Оптимальные перемещения КК с одной круговой орбиты на другую
- Определение характеристической скорости двух импульсного оптимального маневра
- Двух импульсный перелет между компланарными круговыми орбитами
- Методы наведения зенитных управляемых ракет (ЗУР)
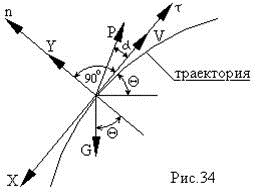
Для того , чтобы определить , как меняется угол Θ составим дифференциальное уравнение движения ракеты в проекции на ось n .
![]() - ускорение движения в проекции на ось n .
- ускорение движения в проекции на ось n .
![]()
Решая это уравнение совместно с уравнением скорости , высоты и дальности мы получим величину Θ , как функцию времени . С другой стороны для того , чтобы ракета выполнила программу угол Θ=Θпрогр .
Выполнение угла Θпрогр обеспечивается выполнением вполне определенного угла атаки α , т.е. α=αпргр=α(t) .
Расчет пассивного (эллиптического) участка траектории .
Постановка задачи .
Примечание :
1. Учитывая , как правило , большие высоты полета на пассивном участке , аэродинамические силы сопротивления не учитываем .
2. По той же причине будем учитывать изменение силы тяжести .
3. 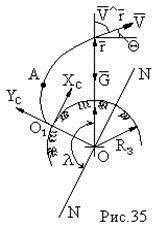 В связи с большими дальностями полета поле тяготения Земли будем рассматривать центральным , т.е. учитывая кривизну Земли .
В связи с большими дальностями полета поле тяготения Земли будем рассматривать центральным , т.е. учитывая кривизну Земли .
4. В пределах расчета одного витка траектории для спутника или расчета траектории ракет класса “Земля — Земля” не будем учитывать вращение Земли .
Дано : VA , ΘA , XA , YA , m=const .
Определить : Lэл — дальность полета на эллиптическом участке траектории ;
Tэл — время полета на эллиптическом участке траектории .
Запишем дифференциальное уравнение движения на эллиптическом участке в векторной форме :
![]()
где g — ускорение действующее на ракету на высоте полета .
![]() - ускорение на уровне Земли .
- ускорение на уровне Земли .
Таким образом получаем :
![]()
![]() - дифференциальное уравнение движения полета ракеты на пассивном участке в векторной форме .
- дифференциальное уравнение движения полета ракеты на пассивном участке в векторной форме .
![]()
Тогда : ![]()
r = RЗ + H , где Н — высота полета ракеты над поверхностью Земли .
Для решения уравнения (1) или (1’) необходимо получить два интеграла .
