Лекция по “Теории полёта”. Часть 2
- Лекция по “Теории полёта”. Часть 2
- Метод последовательных приближений
- Рассмотрим выполнение программного угла Θ
- Интеграл момента количества движения
- Интеграл энергии
- Уравнение траектории пассивного участка
- Уравнение эллиптического участка траектории
- Время полета ракеты на эллиптической траектории
- Расчет участка снижения
- Определение оптимального угла траектории
- Орбитальные движения тел . Законы Кеплера .
- Вывод искусственного спутника Земли (ИСЗ) на орбиту
- Кинематические уравнения , связанные с движением ИСЗ
- Траектория полета космических кораблей
- Оптимальные перемещения КК с одной круговой орбиты на другую
- Определение характеристической скорости двух импульсного оптимального маневра
- Двух импульсный перелет между компланарными круговыми орбитами
- Методы наведения зенитных управляемых ракет (ЗУР)
Оптимальные перемещения КК с одной круговой орбиты на другую
Существенным этапом расчета траектории межпланетных перелетов является оптимальный расчет траектории при перелете КК с одной орбиты на другую .
Известно , что эксцентриситет орбит солнечной системы невелик , поэтому в первом приближении можно принять , что планеты вращаются вокруг Солнца по круговым орбитам .
Будем считать , что обе орбиты — орбита старта и орбита назначения — лежат в одной плоскости .
Время необходимое на перелет с одной орбиты на другую неизвестно .
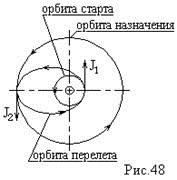
Орбита старта лежит внутри орбиты назначения (рис.48).
Весь процесс перелета с одной орбиты на другую можно разделить на два этапа (фазы) :
на первой фазе в результате приложенного импульса КК , до этого двигающийся по орбите старта , начнет полет по орбите перелета до того момента времени , когда орбита перелета пересечется с орбитой назначения .
Орбиту назначения принимаем круговой .
В точке пересечения орбиты перелета с орбитой назначения прикладывается второй импульс , в результате чего КК начнет двигаться по орбите назначения .
Таким образом мы будем рассматривать двух импульсный маневр перехода . В реальных условиях число импульсов может быть больше двух , тогда маневр перехода называют многоимпульсный .
Оптимальной орбитой перелета с одной круговой орбиты на другую круговую орбиту является орбита эллиптическая , касающаяся орбит старта и назначения в абсидальных точках (крайние точки орбиты) — эллипс Гомана .
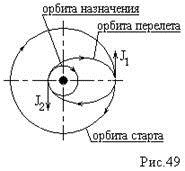
Орбита назначения лежит внутри орбиты старта (рис.49).
При дальнейших расчетах получили , что эллипс Гомана является оптимальной орбитой перелета , когда орбита старта и назначения некруговые (эллиптические) и не пересекаются .
