Лекция по “Теории полёта”. Часть 2
Теория полета космических кораблей .
Орбитальные движения тел .
Законы Кеплера .
Орбитальное движение – это движение только под действием силы тяжести .
Рассмотрим движение КК в поле тяготения , только одного небесного тела . Силу притяжения с достаточной степенью точности можно считать направленной к центру масс этого небесного тела . Такое поле тяготения называется центральным или Кеплеровым полем тяготения .
Известно , что Кеплер в начале XVII века , анализируя результаты наблюдения (движение Марса) , которые провел астроном Тихо де Браго , установил следующие законы движения планет , получившие название законы Кеплера .
Первый закон Кеплера .
Орбита каждой планеты лежит в неподвижной плоскости , проходящей через центр Солнца и является эллипсом в одном из фокусов , которого находится Солнце .
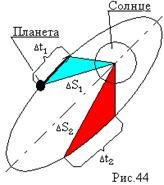
Второй закон Кеплера .
Радиус вектор , соединяющий центры Солнца и планеты , ометает равные площади в равные промежутки времени ΔS1=ΔS2 ; Δt1=Δt2 .
Третий закон Кеплера .
Квадраты времени обращения планет пропорциональны кубам их средних расстояний от Солнца .
