Лекция по “Теории полёта”. Часть 2
- Лекция по “Теории полёта”. Часть 2
- Метод последовательных приближений
- Рассмотрим выполнение программного угла Θ
- Интеграл момента количества движения
- Интеграл энергии
- Уравнение траектории пассивного участка
- Уравнение эллиптического участка траектории
- Время полета ракеты на эллиптической траектории
- Расчет участка снижения
- Определение оптимального угла траектории
- Орбитальные движения тел . Законы Кеплера .
- Вывод искусственного спутника Земли (ИСЗ) на орбиту
- Кинематические уравнения , связанные с движением ИСЗ
- Траектория полета космических кораблей
- Оптимальные перемещения КК с одной круговой орбиты на другую
- Определение характеристической скорости двух импульсного оптимального маневра
- Двух импульсный перелет между компланарными круговыми орбитами
- Методы наведения зенитных управляемых ракет (ЗУР)
Траектория полета космических кораблей
Общие замечания
Космический корабль — летательный аппарат (ЛА) , способный совершать перелеты с одной планеты на другую или с одной орбиты на другую при полете вокруг данной планеты . Весь процесс перелета с одной планеты на другую можно условно разбить на три этапа :
a) полет в близи планеты отправления ;
b) полет в космическом пространстве ;
c) полет в близи планеты назначения .
В общем случае полет на а) и b) проходит частично или полностью в атмосфере , то обстоятельство , что в космическом пространстве атмосфера отсутствует (аэродинамические силы равны нулю) упрощает решение задачи на этапе b) .
Задача движения КК при движении на этапе b) является более сложной , чем движение ИСЗ , т.к. на этом этапе на КК силы притяжения нескольких планет и гравитационное поле действующее на КК изменяется стечением времени .
Решение задачи о движении КК , когда учитывается сила притяжения многих небесных тел может быть получено только численным методом с использованием супермощных ЭВМ .
Задача , когда на КК действует гравитационное поле нескольких планет носит название –“задача “N тел” . В практике расчета КК задачу “N тел” заменяют задачей “двух тел” , в которой всю траекторию полета КК разбивают на отдельные участки и рассматривают движение КК на каждом участке в поле тяготения только одной планеты , т.к. при межпланетных перелетах КК корабль должен преодолевать большие расстояния , то реализовать его движение с непрерывно работающим двигателем практически невозможно (для такого полета запас топлива и стартовый вес самого корабля получился бы нереально большим) . Поэтому в основном межпланетный КК совершает пассивный (баллистический) полет под действием только сил тяготения планет без затрат собственной энергии . В то же время на некоторых участках полета необходима работа двигателей , а именно :
§ на начальном участке ; корабль должен получить нужную скорость и высоту
§ на конечном участке
§ при переходе с одной орбиты на другую
§ на баллистическом при его корректировке
Продолжительность полета с работающим двигателем измеряется минутами или секундами , когда продолжительность пассивного полета — месяцы и годы .
Это позволяет ставить задачу о полете с важным упрощением : заменение распределенного по времени t действие силы тяги двигателей на мгновенное сообщение КК соответствующего импульса тяги 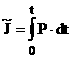 .
.
Результатом приложения ![]() является мгновенное изменение скорости КК при неизменных его координатах .
является мгновенное изменение скорости КК при неизменных его координатах .
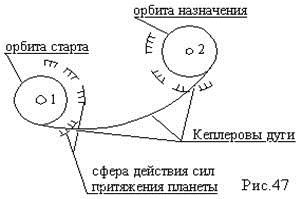
В связи с упрощениями , траектория КК состоит из отрезков Кеплеровых дуг (отрезков баллистических кривых полученных в результате решения задачи “двух тел” .
В точках соединения дуг M и N приложены соответствующие импульсы тяги . Точки M и N в общем случае угловые , т.к. действие импульса тяги направленние изменяет .
При решение задачи межпланетного перелета КК необходимо определить :
§ необходимую величину ![]()
§ момент времени , в который этот ![]() должен быть приложен
должен быть приложен
§ определение полной траектории КК
