Лекция по “Теории полёта”. Часть 2
- Лекция по “Теории полёта”. Часть 2
- Метод последовательных приближений
- Рассмотрим выполнение программного угла Θ
- Интеграл момента количества движения
- Интеграл энергии
- Уравнение траектории пассивного участка
- Уравнение эллиптического участка траектории
- Время полета ракеты на эллиптической траектории
- Расчет участка снижения
- Определение оптимального угла траектории
- Орбитальные движения тел . Законы Кеплера .
- Вывод искусственного спутника Земли (ИСЗ) на орбиту
- Кинематические уравнения , связанные с движением ИСЗ
- Траектория полета космических кораблей
- Оптимальные перемещения КК с одной круговой орбиты на другую
- Определение характеристической скорости двух импульсного оптимального маневра
- Двух импульсный перелет между компланарными круговыми орбитами
- Методы наведения зенитных управляемых ракет (ЗУР)
Определение характеристической скорости двух импульсного оптимального маневра
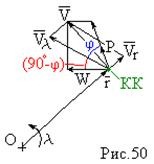
Какую скорость необходимо сообщить КК при двух импульсном маневре перелета .
![]()
Принимаем :
Индекс “1” — это все параметры КК , когда он находится на орбите старта ,а индекс “2” — на орбите назначения .
![]()
U1 — составляющая скорости КК по направлению тяги двигателя непосредственно перед приложением импульса тяги .
W1 — составляющая скорости КК по направлению перпендикулярному вектору тяги , перед приложением импульса тяги .
φ1 — угол между вектором силы тяги и перпендикуляром к радиусу , определяющему положение КК на орбите .

На основании второго закона Кеплера и некоторых преобразований можно записать :
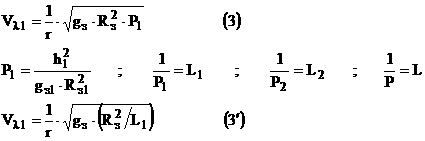
Из уравнения (1) найдем U1
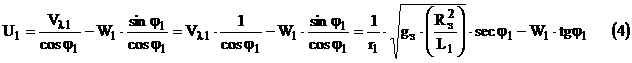
Запишем скорость КК в направлении силы тяги непосредственно после приложения импульса тяги .
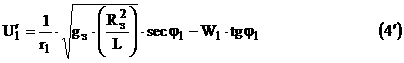
Найдем приращение скорости ![]() в момент старта КК (с орбиты старта)
в момент старта КК (с орбиты старта)
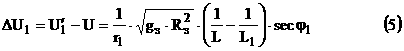
Аналогичным путем находим приращение скорости при приложении импульса тяги в момент прибытия на орбиту назначения .
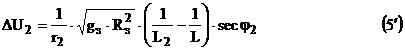
Полная характеристическая скорость двух импульсного маневра равна :
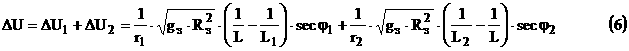
Частный случай :
Будем считать , что орбита старта и назначения круговые , вектор Р направлен по вектору скорости , т.е. φ 1=φ2=0 и что орбита старта лежит внутри орбиты назначения .
После преобразования для этого случая формула (6) примет вид :
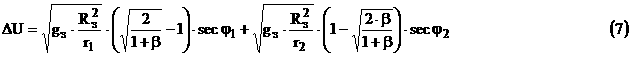
где ![]() .
.
