Лекция по “Теории полёта”. Часть 2

Расчет активного участка траектории БРметодом последовательных приближений

           

При траектории необходимо знать следующие параметры траектории движения ракеты в зависимости от времени :

§  Скорость                               V=V(t) ;

§  Дальность                             X=X(t) ;

§  Высота                                  Y=Y(t) ;

§  Угол траектории                  Θ=Θ(t) .

Допущения для данной задачи :

1.      Траектория полета ракеты плоская кривая .

2.      Пренебрегаем кривизной Земли в пределах дальности АУТ .

3.      Силу тяжести считаем постоянной ,   т.е.   g = const .

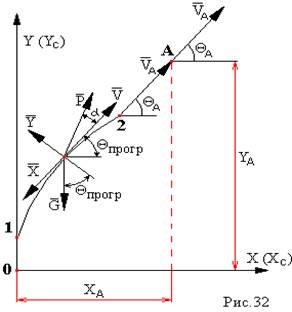
Таким образом траекторию активного участка можно показать так (рис.32) :

 

01 — вертикальный участок траектории ;

12 — программный участок траектории ;

2А — наклонный (или прямой) участок траектории .

            В качестве критерия точки 1 служит скорость , которая должна быть достигнута ракетой в этой точке (≈55 м/с) . На программном участке траектории угол  Θ=Θ_прогр .

Θ_прогр=At²+Bt+C       — задается в общем виде.

Коэффициенты А , В , С  определяются из трех граничных условий в точках 1 и 2 .

точка 1                      

точка 2                                              находим А,В,С имея ввиду ,

точка 2                                               что Θ_А дано .

Таким образом необходимо определить параметры движения ракеты на активном участке . Для этого составим систему уравнений :

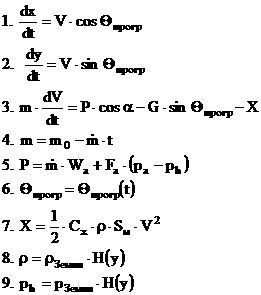
где      Н(у) — функция , зависящая от высоты полета ;

            р_Земли =101340    .

Т.к. α для БР при их движении на АУТ небольшой (α≤10^о) , то можно принять , что

cosα≈1 ; sin α ≈α . Приведенная выше система является нелинейной , замкнутой и ее можно решить любым численным методом .

 

 

 

• Prev
• Вперёд >>