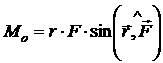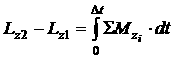Механика. Лекции по физике
- Механика. Лекции по физике
- КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
- ДИНАМИКА. ЗАКОНЫ НЬЮТОНА
- СИЛЫ В МЕХАНИКЕ
- ИМПУЛЬС ТЕЛА. ИМПУЛЬС СИЛЫ. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА.
- ЦЕНТР МАСС. ЗАКОН ДВИЖЕНИЯ ЦЕНТРА МАСС.
- ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
- РАБОТА И ЭНЕРГИЯ.
- ОСНОВНЫЕ ЗАКОНЫ АЭРО- И ГИДРОМЕХАНИКИ.
- ОСНОВЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ.
- Примеры решения задач
- Тема «Законы Ньютона»
- Тема «Импульс тела. Центр масс»
- Тема «Динамика вращательного движения»
- Тема «Работа. Механическая энергия»
- Тема «Уравнения гидродинамики»
Вращающее действие силы определяется ее моментом. Моментом ![]() силы
силы ![]() относительно какой-либо точки
относительно какой-либо точки ![]() называется векторное произведение
называется векторное произведение
![]() — радиус-вектор, проведенный из точки
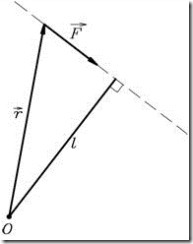
— радиус-вектор, проведенный из точки ![]() в точку приложения силы (рис.5). Единица измерения момента силы
в точку приложения силы (рис.5). Единица измерения момента силы ![]() .
.
Величина момента силы
или можно записать
где ![]() — плечо силы ( кратчайшее расстояние от точки
— плечо силы ( кратчайшее расстояние от точки ![]() до линии действия силы).
до линии действия силы).
Рис.5.
Момент силы относительно какой-либо точки равен нулю, если линия действия силы проходит через эту точку.
Проекция вектора ![]() на какую-либо ось, например, ось z, называется моментом
на какую-либо ось, например, ось z, называется моментом ![]() силы
силы ![]() относительно этой оси. Чтобы определить момент силы
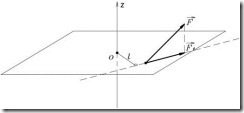
относительно этой оси. Чтобы определить момент силы ![]() относительно оси, сначала проецируют силу на плоскость, перпендикулярную оси (рис.6), а затем находят момент этой проекции относительно точки пересечения оси с перпендикулярной ей плоскостью. Если линия действия силы параллельна оси, или пересекает ее, то момент силы относительно этой оси равен нулю.
относительно оси, сначала проецируют силу на плоскость, перпендикулярную оси (рис.6), а затем находят момент этой проекции относительно точки пересечения оси с перпендикулярной ей плоскостью. Если линия действия силы параллельна оси, или пересекает ее, то момент силы относительно этой оси равен нулю.
Рис.6.
2. Момент инерции тела.
Моментом инерции ![]() тела относительно какой-либо оси z называется сумма произведений масс точек этого тела на квадраты расстояний от этих точек до оси
тела относительно какой-либо оси z называется сумма произведений масс точек этого тела на квадраты расстояний от этих точек до оси
![]() — масса
— масса ![]() -той точки ,
-той точки , ![]() — кратчайшее расстояние от
— кратчайшее расстояние от ![]() -той точки до оси z.
-той точки до оси z.
Для сплошных тел момент инерции определяется через интеграл
![]() - расстояние от элемента
- расстояние от элемента ![]() массы тела до оси z.
массы тела до оси z.
Моменты инерции однородных тел простой геометрической формы обычно рассчитывают по формуле (43), а сложной определяют экспериментально. В таблице 1 приведены моменты инерции некоторых тел.
Теорема Штейнера. Если для какого-либо тела известен его момент инерции ![]() относительно оси
относительно оси ![]() , проходящей через центр масс
, проходящей через центр масс ![]() тела, то момент инерции этого тела относительно оси
тела, то момент инерции этого тела относительно оси ![]() , параллельной
, параллельной ![]() , равен
, равен
![]() - масса тела,
- масса тела, ![]() - кратчайшее расстояние между осями
- кратчайшее расстояние между осями ![]() и
и ![]() .
.
2. Основной закон динамики вращательного движения.
Для тела, вращающегося вокруг оси z,
![]() — момент инерции тела относительно оси вращения z,
— момент инерции тела относительно оси вращения z, ![]() — угловое ускорение тела,
— угловое ускорение тела, ![]() — сумма моментов сил, приложенных к телу, и рассчитанных относительно оси вращения,
— сумма моментов сил, приложенных к телу, и рассчитанных относительно оси вращения, ![]() - индекс суммирования. Уравнение (45) представляет собой основной закон динамики вращательного движения.
- индекс суммирования. Уравнение (45) представляет собой основной закон динамики вращательного движения.
3. Условия равновесия тел.
Из 2-го закона Ньютона ![]() и основного уравнения динамики вращательного движения
и основного уравнения динамики вращательного движения ![]() следуют условия равновесия тел: для покоящегося тела
следуют условия равновесия тел: для покоящегося тела
1) сумма действующих на тело сил должна быть равной нулю,
или, если использовать проекции сил, то
2) сумма моментов сил относительно любой точки тела должна быть равна нулю
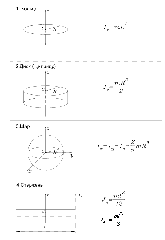
Таблица 1. Моменты инерции некоторых тел.
 |
Моментом ![]() импульса материальной точки массой
импульса материальной точки массой ![]() , движущейся со скоростью
, движущейся со скоростью ![]() , относительно какой-либо точки отсчета
, относительно какой-либо точки отсчета ![]() , называют векторное произведение
, называют векторное произведение
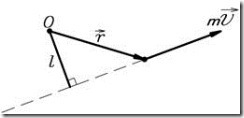
![]() - радиус-вектор материальной точки (рис.7),
- радиус-вектор материальной точки (рис.7), ![]() — ее импульс.
— ее импульс.
Рис.7.
Величина момента импульса материальной точки
где ![]() -кратчайшее расстояние от линии вектора
-кратчайшее расстояние от линии вектора ![]() до точки
до точки ![]() .
.
Для вращающегося тела момент импульса ![]() относительно оси вращения
относительно оси вращения ![]()
равен
![]() - момент инерции тела относительно оси
- момент инерции тела относительно оси ![]() и
и ![]() — его угловая скорость.
— его угловая скорость.
Скорость изменения момента импульса системы тел равна сумме моментов сил, приложенных к этой системе
Тогда
Если моменты сил постоянны, то уравнение (50) можно записать в виде
т.е. изменение момента импульса системы тел относительно какой-либо оси ![]() равно сумме моментов сил, действующих на эту систему, умноженной на время
равно сумме моментов сил, действующих на эту систему, умноженной на время ![]() .
.
Отсюда следует закон сохранения момента импульса: момент импульса ![]() системы тел относительно оси
системы тел относительно оси ![]() сохраняется, если сумма моментов сил
сохраняется, если сумма моментов сил ![]() , действующих на эту систему, равна нулю.
, действующих на эту систему, равна нулю.