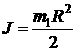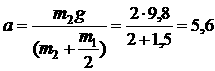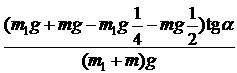Лекции для студентов

Механика. Лекции по физике

Тема «Динамика вращательного движения»

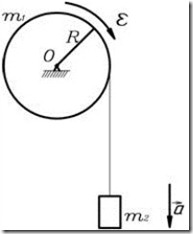
Пример 7. На барабан массой =3 кг намотан шнур, к концу которого привязан груз массой =2 кг (рис.18). Найти ускорение груза и силу натяжения шнура, считая барабан однородным диском. Трением пренебречь.

 

Дано: =3 кг, =2 кг,

барабан — диск. Найти: , .

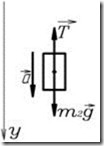
Решение. На груз действуют

сила тяжести и сила

натяжения шнура (рис.19) .

Т.к. груз совершает

поступательное движение,

запишем для него 2-ой закон Ньютона Рис.18

в проекции на ось y, направленную

вертикально вниз, Рис.18.

. (1)

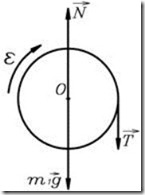
На барабан действуют сила натяжения , сила тяжести и реакция опоры (рис.20).

Рис.19. Рис.20.

Т.к. барабан вращается, воспользуемся основным законом динамики вращательного движения и запишем его относительно оси вращения, проходящей через точку :

, (2)

 — радиус барабана. Моменты сил и относительно точки равны нулю.

Т. к. барабан — однородный диск, его момент инерции

.

Угловое ускорение барабана . Подставив и в уравнение (2), получаем

. (3)

Отсюда . (4)

Подставим в (1):

.

Тогда .

Отсюда ускорение

м/с².

Сила натяжения шнура из уравнения (4):

Н.

Ответ: м/c² , Н.

Пример 8. Лестница массой =16 кг приставлена к вертикальной стене под углом 20^° к ее поверхности. На лестнице на расстоянии ее длины , от нижнего конца, стоит человек массой =75 кг. Каким должен быть коэффициент трения между основанием лестницы и поверхностью пола, чтобы лестница не соскользнула? Трением между лестницей и стенкой пренебречь.

Дано: =16 кг, =75 кг, =20°, . Найти: .

Рис.21.

Решение. Обозначим - длина лестницы. На лестницу с человеком действуют сила тяжести лестницы , человека , сила трения и реакции опор и (рис.21).

Т.к. система находится в равновесии, то сумма действующих на нее сил и моментов сил должна быть равна нулю.

Запишем условие равенства нулю суммы сил в проекции на ось y:

.

Отсюда .

Запишем условие равенства нулю моментов сил, относительно точки :

.

Сокращая на и учитывая, что , получаем

.

Отсюда ==

=

Ответ: .