Лекции для студентов

Электричество и магнетизм. Часть 4

5.3. Вынужденные электрические колебания. Метод векторных диаграмм.

Если в цепь электрического контура, содержащего емкость, индуктивность и сопротивление, включить источник переменной ЭДС (рис.16.5), то в нем, наряду с собственными затухающими колебаниями, возникнут незатухающие вынужденные колебания. Частота этих колебаний совпадает с частотой изменения переменной ЭДС.

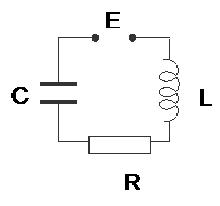
Рис.16.5. Последовательный колебательный RLC-контур.

Чтобы получить уравнение вынужденных колебаний, надо, согласно второму правилу Кирхгофа, приравнять сумму падений напряжений на элементах контура приложенной ЭДС:

или

где Е₀ - амплитуда переменной ЭДС; ω — ее циклическая частота.

Интересующее нас частное решение этого дифференциального уравнения имеет вид:

где

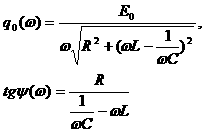
Решение соответствующего однородного уравнения, как мы видели в п.5.2, представляет собой свободные затухающие колебания, которые с течением времени становятся исчезающе малыми, и их можно в дальнейшем не учитывать.

Выпишем формулы для силы тока в цепи и падений напряжений на каждом из элементов контура.

Сила тока: ,

.

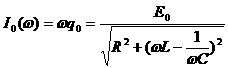По аналогии с законом Ома для полной цепи по постоянному току величину

называют полным сопротивлением цепи по переменному току. Эта величина представляет собой модуль комплексного сопротивления , называемого также импедансом цепи. Сопротивление R называют активным сопротивлением (на нем выделяется тепло). Чисто мнимые сопротивления ωL и называют соответственно индуктивным и емкостным реактивными сопротивлениями (на них тепло не выделяется).

Напряжение на сопротивлении R:

,

.

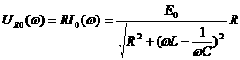Напряжение на конденсаторе С:

,

.

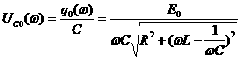Напряжение на катушке индуктивности L:

,

.

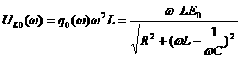Сравнивая написанные формулы, видим, что изменение напряжения на сопротивлении следует за изменением силы тока в цепи без отставания или опережения по фазе, изменение напряжение на конденсаторе отстает по фазе на , а на индуктивности опережает по фазе на изменение тока. Наглядно это можно изобразить с помощью векторной диаграммы (рис.16.6), вещественная ось которой (ось Х) совпадает с осью токов. Длина каждого вектора на этой диаграмме дает амплитуду соответствующего напряжения, а угол, который составляет данный вектор с осью токов — сдвиг фазы по отношению к изменению силы тока в цепи.

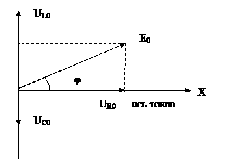
Рис.16.6. Векторная диаграмма для последовательного RLC-контура.

Амплитуда суммарного напряжения на всех элементах контура, равная амплитуде Е₀ действующей в контуре ЭДС, является результатом векторного сложения символических напряжений и . Этот вектор образует с осью токов угол , показывающий разность фаз между током и ЭДС. Тангенс этого угла равен:

.
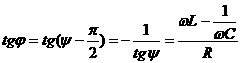