Лекции для студентов

Электричество и магнетизм. Часть 4

5.4. Резонансные явления в колебательном контуре. Резонанс напряжений и резонанс токов.

Как следует из приведенных формул, при частоте переменной ЭДС ω, равной

,

амплитудное значение силы тока в колебательном контуре, принимает максимальное значение . При этом амплитуда напряжения на активном сопротивлении R также максимальна и равна U_R0 =I_0maxR =E₀. Падения напряжения на емкости U_C и индуктивности U_L одинаковы по амплитуде, но противоположны по фазе, и они взаимно компенсируют друг друга. Это явление, имеющее место в последовательномколебательном контуре, изображенном на рис.16.5, называется резонансом напряжений. Векторная диаграмма, соответствующая этому случаю, показана на рис.16.7.

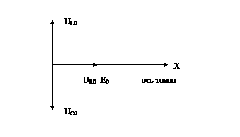
Рис.16.7. Векторная диаграмма при резонансе напряжений.

Максимальное значение амплитуды напряжения на конденсаторе U_C0(ω) достигается при частоте

.

Резонансные кривые для U_C0(ω) представлены на рис.16.8. Максимум получается тем выше и острее, чем меньше коэффициент затухания β, то есть чем меньше активное сопротивление R и больше индуктивность контура L.

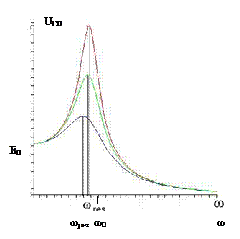Рис.16.8. Резонансные кривые U_C0(ω).

Если источник переменной ЭДС подключить параллельно конденсатору, то получим колебательный контур, который называется параллельным(рис.16.9).

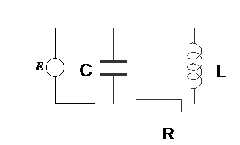
Рис.16.9. Параллельный колебательный RLC-контур.

В таком контуре при наблюдается другое резонансное явление, получившее название резонанса токов. При резонансе токов токи, текущие через емкость и индуктивность одинаковы по амплитуде, но противоположны по фазе. При этом общий ток в цепи ЭДС близок к нулю, хотя токи в самом контуре могут быть очень велики. Векторная диаграмма, соответствующая этому случаю, приведена на рис.16.10.

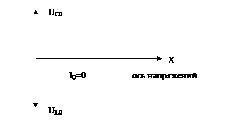
Рис.16.10. Векторная диаграмма при резонансе токов.

Можно показать, что при резонансе токов полное сопротивление Z(ω) параллельного контура максимально и равно чисто активному сопротивлению R. Резонансная частота, при которой Z(ω) максимально, определяется из условия равенства нулю реактивной части комплексного сопротивления :

ωL(1 — ω²LC) — ωCR² = 0 ,

откуда

.

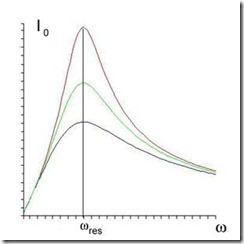Резонансные кривые для амплитудных значений I_C0(ω) тока, текущего через конденсатор, приведены на рис.16.11.

	IC0
		ω
		ωрез ω0

Рис.16.11. Резонансные кривые I_C0(ω).

Резонансные явления в колебательных контурах широко используются в электро- и радиотехнике (резонансные усилители, частотные фильтры и другие). В частности, явление резонанса используется для выделения из сложного сигнала нужной частотной составляющей. Настроив контур (путем изменения его параметров C и/или L) на одну из выбранных частот, можно получить на конденсаторе напряжение, в Q раз превышающее величину напряжения данной частотной составляющей (см. рис.16.8). Такой процесс осуществляется, например, при настройке радиоприемника на нужную длину волны.