Лекции для студентов

Электричество и магнетизм. Часть 4

5.9. Стоячие волны.

При наложении двух встречных волн с одинаковой амплитудой возникают стоячие волны. Возникновение стоячих волн имеет место, например, при отражении волн от преграды. Падающая на преграду волна и бегущая ей навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну (рис.17.3).

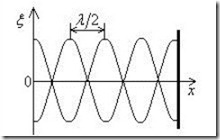
Рис.17.3. Образование стоячей волны.

Стоячие волны бывают продольные (колебания стержней, звуковые волны в резонаторе музыкального инструмента) и поперечные (колебания закрепленной на концах натянутой струны, капиллярные волны на поверхности жидкости).

Рассмотрим две плоские монохроматические волны, распространяющиеся навстречу друг другу. Уравнения волн имеют вид:

,

.

Складывая эти уравнения и преобразовывая результат по формуле для суммы косинусов, получим:

.

Заменив в этом выражении волновое число k его значением , придадим ему следующий вид:

,

где  — амплитуда колебаний.

Написанное уравнение — есть уравнение стоячей волны. Из него видно, что в стоячей волне колебания в каждой точке происходят с той же частотой ω, что и у налагающихся волн. При этом амплитуда колебаний зависит от координаты точки х.

В точках с координатами амплитуда колебаний максимальна и равна 2a. Эти точки называются пучностями стоячей волны.

В точках с координатами амплитуда колебаний равна нулю. Эти точки называют узлами стоячей волны.

Расстояние между соседними пучностями (узлами) составляет . Сами пучности и узлы сдвинуты относительно друг друга на четверть длины волны (рис.17.3). Фазы колебаний по разные стороны от узла отличаются на π, то есть точки, лежащие по разные стороны от узла, колеблются в противофазе, а все точки, заключенные между двумя соседними узлами, колеблются в одной фазе.

Отметим, что в стоячей волне дважды за период колебаний происходит переход кинетической энергии от узла (где скорость равна нулю) к пучности (где она максимальна) и обратно. То же происходит и с потенциальной энергией, но в обратной последовательности по отношению к кинетической энергии. В результате средний поток энергии через любое сечение в стоячей волне равен нулю.