Электричество и магнетизм. Часть 4
- Электричество и магнетизм. Часть 4
- 4.12. Вихревое электрическое поле. Первое уравнение Максвелла.
- 4.13. Второе уравнение Максвелла, третье уравнение Максвела
- 4.15. Четвертое уравнение Максвелла.
- 4.16. Дифференциальная форма уравнений Максвелла.
- 4.17. Замкнутая система уравнений Максвелла. Материальные уравнения.
- 4.18. Следствия из уравнений Максвелла. Электромагнитные волны. Скорость света.
- Колебания и волны: электромагнитные колебания
- 5.2. Свободные затухающие колебания. Добротность колебательного контура.
- 5.3. Вынужденные электрические колебания. Метод векторных диаграмм.
- 5.4. Резонансные явления в колебательном контуре. Резонанс напряжений и резонанс токов.
- 5.5. Волновое уравнение. Типы и характеристики волн.
- 5.6. Электромагнитные волны.
- 5.7. Энергия и импульс электромагнитной волны. Вектор Пойнтинга.
- 5.8. Упругие волны в твердых телах. Аналогия с электромагнитными волнами.
- 5.9. Стоячие волны.
- 5.10. Эффект Допплера.
5.6. Электромагнитные волны.
Из уравнений Максвелла следует, что если возбудить с помощью зарядов переменное электрическое или магнитное поле, в окружающем пространстве возникнет последовательность взаимных превращений электрического и магнитного полей, распространяющихся в виде электромагнитной волны. Для однородной нейтральной (ρ=0) и непроводящей (![]() ) среды с постоянными проницаемостями ε и μ, волновое уравнение, описывающее электромагнитную волну, распадается на два независимых векторных уравнения соответственно для электрического
) среды с постоянными проницаемостями ε и μ, волновое уравнение, описывающее электромагнитную волну, распадается на два независимых векторных уравнения соответственно для электрического ![]() и магнитного
и магнитного ![]() полей:
полей:
![]() ,
, ![]() .
.
Фазовая скорость электромагнитной волны v определяется по формуле:
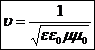 .
.
Для вакуума (ε = μ = 1) по этой формуле получается:
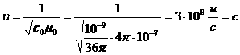 .
.
Таким образом, в вакуумефазовая скорость электромагнитной волны совпадает со скоростью света. В среде с постоянными проницаемостями ε и μ
![]()
Рассмотрим плоскую электромагнитную волну, распространяющуюся вдоль оси х, перпендикулярной к волновым поверхностям. В этом случае, очевидно, поля ![]() и
и ![]() не зависят от координат y и z. Соответствующие уравнения Максвелла, записанные для этого случая, приводят к следующим скалярным волновым уравнениям:
не зависят от координат y и z. Соответствующие уравнения Максвелла, записанные для этого случая, приводят к следующим скалярным волновым уравнениям:
![]() ,
, ![]() .
.
Простейшими решениями этих уравнений являются функции
Ey(x,t) = Em cos(ωt — kx);
Hz(x,t) = Hm cos(ωt — kx),
совместность которых обеспечивается условиями, вытекающими из уравнений Максвелла
kEm = μμ0ωHm ,
εε0ωEm = kHm .
Отсюда следует, что колебания электрического и магнитного векторов в электромагнитной волне происходят с одинаковой фазой, а амплитуды этих векторов связаны между собой соотношением:
![]() .
.
Из последней формулы вытекает, в частности, что отношение Em к Hm для электромагнитной волны, распространяющейся в вакууме:
![]() .
.
В векторном виде уравнения плоской электромагнитной волны записываются как:
![]() ,
,
![]() .
.
На рис.17.2 показана мгновенная картина плоской электромагнитной волны в данный момент времени t.
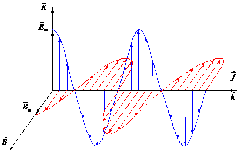
Рис.17.2. Структура плоской электромагнитной волны.
Как видно из рис.17.2, векторы ![]() и
и ![]() (на рисунке
(на рисунке ![]() ) образуют с направлением распространения волны
) образуют с направлением распространения волны ![]() правовинтовую систему, то есть электромагнитная волна является поперечной. В фиксированной точке пространства электромагнитное поле в волне изменяется по гармоническому закону.
правовинтовую систему, то есть электромагнитная волна является поперечной. В фиксированной точке пространства электромагнитное поле в волне изменяется по гармоническому закону.
