Лекции для студентов

Электричество и магнетизм. Часть 4

5.8. Упругие волны в твердых телах. Аналогия с электромагнитными волнами.

Законы распространения упругих волн в твердых телах вытекают из общих уравнений движения однородной упруго деформированной среды:

,

где ρ – плотность среды; u_i — компоненты вектора упругого смещения; σ_{ik =} c_iklmε_lm — тензор напряжений; - тензор деформации; c_iklm – тензор упругих модулей.

Отсюда следует, что вектор упругого смещения удовлетворяет волновому уравнению вида:

.

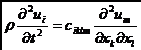Если искать решение этого уравнения в виде плоской монохроматической волны

,

то ему можно придать вид:

,

где  — тензор приведенных упругих модулей; - единичный вектор волновой нормали; c = ω/k — фазовая скорость упругой волны.

Полученное уравнение является основным для всей теории упругих волн в твердых телах, и носит название уравнения Кристоффеля. Из него, в частности, следует, что в анизотропных твердых телах (кристаллах) по любому направлению могут распространяться три упругие волны, которые в общем случае не являются ни чисто продольными, ни чисто поперечными. Фазовые скорости их также различны.

Изотропные твердые тела характеризуются только двумя упругими модулями — модулем Юнга E и модулем сдвига G. В таких телах две из трех упругих волн всегда являются чисто поперечными и имеют одинаковуюфазовую скорость c_t; третья волна является чисто продольной и имеет свою фазовую скорость c_l > c_t. В данном случае исходное волновое уравнение распадается на два независимых волновых уравнения для двух поперечных волн и одной продольной волны :

; ,

где - фазовая скорость поперечной волны; - фазовая скорость продольной волны.

Как и электромагнитные волны, упругие волны переносят энергию и импульс. Перенос энергии в упругой волне осуществляется за счет потока вектора Умова , аналогичного вектору Пойнтинга , и имеющему смысл плотности потока энергии. Дифференциальное уравнение закона сохраненияэнергии для упругого поля имеет аналогичный вид:

,

где

 —

плотность энергии упругой волны, которая слагается из кинетической энергии колеблющихся частиц среды и потенциальной энергии упругой деформации;

-

компоненты вектора Умова (Умов Н.А., 1846-1915).

Альтернативный подход к описанию закономерностей распространения упругих волн в кристаллах основан на представлении первичного волнового уравнения второго порядка системой дифференциальных уравнений в частных производных первого порядка от вектора смещения (Наими Е.К., Хзарджян С.М., 1978). При этом уравнения для поперечных компонент вектора смещения оказываются полностью аналогичными уравнениям Максвелла для электромагнитного поля в вакууме, а для продольных компонент — аналогичными уравнениям плазменных колебаний. Соответствующие уравнения записываются в виде:

для поперечных компонент

для продольных компонент

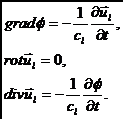
Преимуществом данного подхода является то, что он открывает возможность исследования упругих волновых процессов в кристаллах на основе математического аппарата, разработанного в электродинамике сплошных сред.