Электричество и магнетизм. Часть 4
- Электричество и магнетизм. Часть 4
- 4.12. Вихревое электрическое поле. Первое уравнение Максвелла.
- 4.13. Второе уравнение Максвелла, третье уравнение Максвела
- 4.15. Четвертое уравнение Максвелла.
- 4.16. Дифференциальная форма уравнений Максвелла.
- 4.17. Замкнутая система уравнений Максвелла. Материальные уравнения.
- 4.18. Следствия из уравнений Максвелла. Электромагнитные волны. Скорость света.
- Колебания и волны: электромагнитные колебания
- 5.2. Свободные затухающие колебания. Добротность колебательного контура.
- 5.3. Вынужденные электрические колебания. Метод векторных диаграмм.
- 5.4. Резонансные явления в колебательном контуре. Резонанс напряжений и резонанс токов.
- 5.5. Волновое уравнение. Типы и характеристики волн.
- 5.6. Электромагнитные волны.
- 5.7. Энергия и импульс электромагнитной волны. Вектор Пойнтинга.
- 5.8. Упругие волны в твердых телах. Аналогия с электромагнитными волнами.
- 5.9. Стоячие волны.
- 5.10. Эффект Допплера.
5.2. Свободные затухающие колебания. Добротность колебательного контура.
Всякий реальный колебательный контур обладает сопротивлением (рис.16.3). Энергия электрических колебаний в таком контуре постепенно расходуется на нагревание сопротивления, переходя в джоулево тепло, вследствие чего колебания затухают.
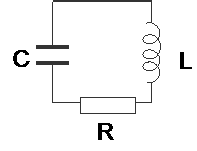
Рис.16.3. Колебательный RLC-контур.
Уравнение свободных затухающих колебаний можно получить, исходя из того, что в отсутствии внешнего источника напряжения, сумма падений напряжений на индуктивности, емкости и сопротивлении равна нулю для любого момента времени:
или, поскольку![clip_image183[1]](/images/stories/clip_image183-1_thumb.gif "clip_image183[1]"){kind=small}
,
.
Введя обозначение
,
этому уравнению можно придать вид:
,
где 
.
Решение полученного уравнения имеет вид:
 |
||
 |
где
 |
Мы видим, что частота свободных затухающих колебаний ω′ меньше собственной частоты ω0. Подставив значения ω0 и β, получим:
Амплитуда затухающих колебаний заряда конденсатора q0(t) уменьшается со временем по экспоненциальному закону (рис.16.4). Коэффициент β называется коэффициентом затухания.
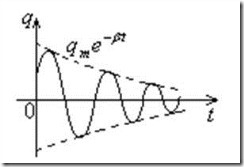
Рис.16.4. Изменение заряда конденсатора со временем в RLC-контуре.
Затухание колебаний принято характеризовать декрементом колебаний λ, определяемым как:
.
Легко видеть, что декремент колебаний обратен по величине числу колебаний Ne, совершаемых за время, в течение которого амплитуда колебаний уменьшается в е раз: λ=1/Ne. Добротностью колебательного контура называется величина:
Из этой формулы видно, что добротность тем выше, чем меньше коэффициент затухания β. При малых затуханиях (λ<<1) можно приближенно считать, что
.
Амплитуда тока в контуре, как и заряд на конденсаторе, убывает со временем по закону 
. Энергия W, запасенная в контуре, пропорциональна квадрату амплитуды тока (или квадрату напряжения на конденсаторе). Следовательно, W убывает со временем по закону e-2βt. Относительное уменьшение энергии за период колебания Т (при малом затухании) есть:
.
Таким образом, потери энергии в колебательном контуре тем меньше, чем выше его добротность.
