Лекции для студентов

Теория автоматического управления. Лекция 3: Математическое описание автоматических систем управления

Таблица 2.1

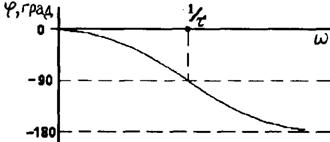
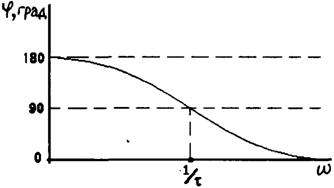
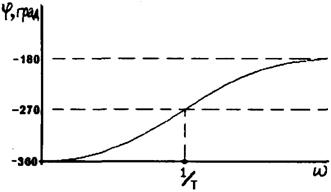
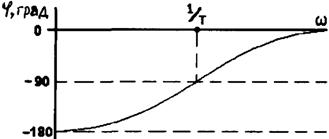
Элементарные неминимально-фазовые звенья

Передаточная функция W	Выражение ФЧХ	График ЛФЧХ
1	2	3

1	2	3

2.7.2. Интегрирующие звенья

Идеальное интегрирующее звено

Уравнение и передаточная функция

,
или при нулевых начальных условиях

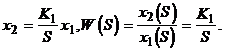(2.48)

Частотная передаточная функция

. (2.49)

Частотные характеристики

.

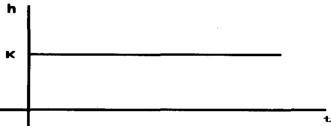
Переходная характеристика

 

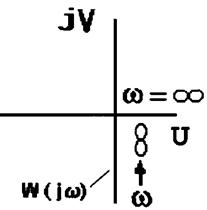
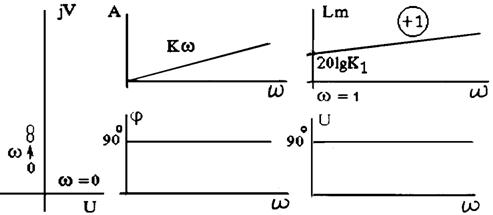
АФЧХ (рис.2.28,а) интегрирующего звена совпадает с отрицательной мнимой полуосью.

а	б	в
Рис. 2.28

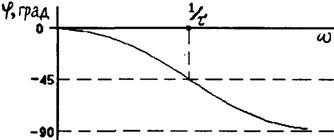
Логарифмическая амплитудная частотная характеристика (рис.2.28,б) имеет вид

. (2.50)

Отметим, что на частоте w=1 ЛАХ , а на частоте ЛАХ пересекает ось частот, так как .

ЛАХ интегрирующего звена имеет наклон -20 дБ/дек. Для построения ЛАХ линию с таким наклоном проводят либо через точку с абсциссой w=1 и ординатой , либо через точку с абсциссой и ординатой .

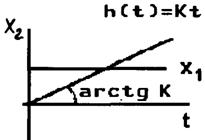
ФЧХ не зависит от частоты, и фазовый сдвиг равен -90° на всех частотах. Переходная характеристика h(t) представляет собой прямую, проходящую через начало координат с угловым коэффициентом наклона (рис.2.28.в).

Рис. 2.29

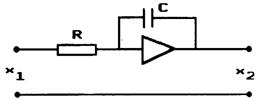
Примером интегрирующих звеньев могут служить двигатели, если выходной величиной является угол поворота вала; операционный усилитель в режиме интегратора (рис.2.29).

Инерционное интегрирующее звено

Уравнение и передаточная функция звена:

(2.51)

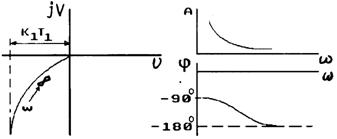
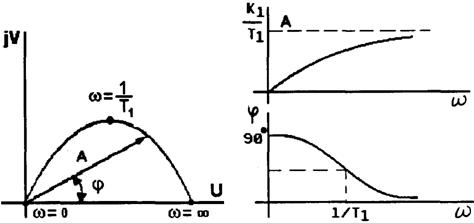
Амплитудно-фазовая частотная характеристика (рис.2.30)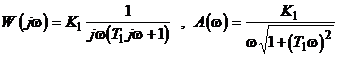

Рис. 2.30

ВЧХ и МЧХ имеют вид

,

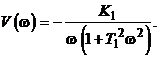
Из выражений ВЧХ и МЧХ следует, что при

.

Рис. 2.31

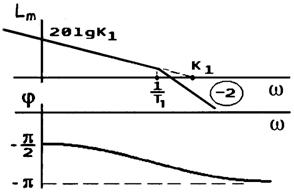
ЛАЧХ описывается выражением

Асимптотическая ЛАЧХ и ЛФЧХ звена представлены на рис.2.31.

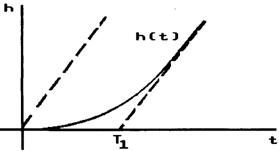
Переходная функция как решение уравнения звена имеет вид

и изображена на рис.2.32.

Рис. 2.32

Из рисунка видно, что за счет постоянной времени, вместо идеального интегрирования, здесь

получается интегрирование с инерционным за­паздыванием. Примером инерционного интегрирующего звена может служить электродвигатель при учете электромеханической постоянной, если выходной величиной считать угол поворота вала двигателя.

Следует обратить внимание на следующую важную особенность позиционных и интегрирующих звеньев: асимптоты ЛАЧХ этих звеньев в области высших частот имеют отрицательные наклоны, крутизна которых определяется порядком полинома знаменателя передаточной функции звена; фазовые сдвиги, вносимые этими звеньями, также отрицательны.

2.7.3. Дифференцирующие звенья

Идеальное дифференцирующее звено

Уравнение и передаточная функция звена

(2.52)

Амплитудно-фазовая частотная характеристика (рис.2.33.а)

Идеальным такое звено называют потому, что степень полинома числителя переда­точной функции (m=1) больше степени полинома знаменателя (n=0), что, в свою очередь, свидетельствует о бесконечно большом усилении () в области высоких частот (), что в реальных звеньях физически невозможно.

В реальных системах такой вид характеристики звена возможен лишь в ограниченной полосе частот.

а б в Рис. 2.33 Частотные характеристики идеального дифференцирующего звена

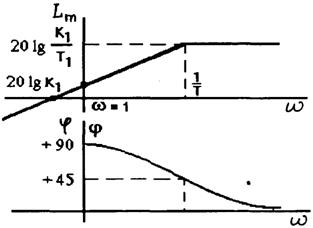
Логарифмические частотные характеристики (рис.2.33,в)

Для построения ЛАХ линию наклоном +20 дБ/дек проводят через точку на частоте либо через точку на частоте

Переходная функция представляет собой d - функцию:

 

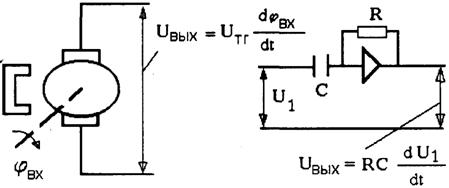
Примером такого звена может служить тахогенератор (рис.2.34,а) — маломощный электрогенератор, выходное напряжение которого пропорционально угловой скорости вращения якоря (производной угла поворота якоря ) или дифференцирующий операционный усилитель (рис.2.34,б).

Еще раз подчеркиваем, что дифференцирующими свойствами эти устройства обладают в ограниченной полосе частот, где пренебрежимо мало влияние инерционных составляющих передаточных функций звеньев.

а б Рис. 2.34

Инерционное (реальное) дифференцирующее звено

Уравнение и передаточная функция звена

(2.53)

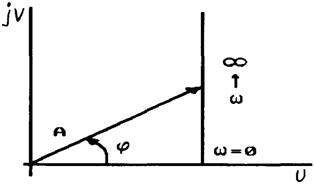
Амплитудно-фазовая частотная характеристика (рис.2.35.а) звена

 

 

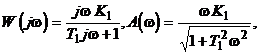
Рис. 2.35 Частотные характеристики реального дифференцирующего звена

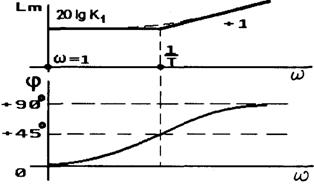
Логарифмические частотные характеристики (рис.2.36)

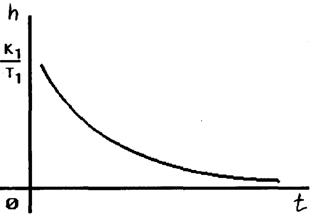
Переходная функция (рис.2.37)

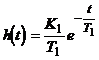
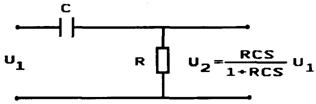
Примером такого звена может служить дифференцирующая R-C цепь (рис.2.38).

Рис. 2.36	Рис. 2.37
Рис. 2.38

Форсирующее звено (идеальное звено с введением производной)

Форсирующим звеном первого порядка называют звено, которое описывается урав­нением

Передаточная функция

(2.54)

Это звено так же, как и апериодическое характеризуется двумя параметрами: постоянной времени и передаточным коэффициентом  

Частотная передаточная функция (рис.2.39,а)

 

 

ВЧХ и МЧХ имеет вид

Уравнение асимптотической ЛАХ форсирующего звена

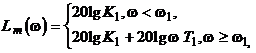
где частота сопряжения.

а	б
Рис. 2.39

Асимптотическая ЛАЧХ после частоты сопряжения имеет "+l" наклон или +20 дБ/дек.

Рис. 2.40

ЛФЧХ форсирующего звена можно получить зеркальным отражением относительно оси частот ЛФЧХ апериодического звена и пользоваться теми же номограммой и шаблонами.

Переходная функция (рис. 2.40)

 . 

Форсирующее звено второго порядка

Уравнение и передаточная функция

при условии, что .

Амплитудно-фазовая частотная характеристика (рис.2.41)

Рис. 2.41

Рис. 2.42

Выражения и графики для ЛАЧХ и ЛФЧХ могут быть получены из аналогичных графиков колебательного звена (при тех же значениях,) путем зеркального отображения относительно оси частот при K=1. 

Следует отметить, что при частотах, превышающих сопрягающую частоту, ЛАЧХ форсирующего звена второго порядка имеет "+2" наклон или +40 де/дек.

Если , то передаточная функция этого звена представляется в виде произведения двух форсирующих звеньев первого порядка.

2.7.4. Звено чистого запаздывания

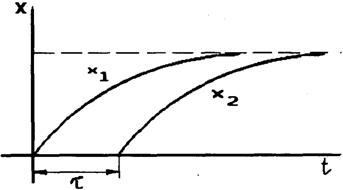
Выходная величина в звеньях чистого запаздывания воспроизводит входную с отставанием по времени (рис.2.43).

Таким звеньям соответствуют объекты с распределенными параметрами, например длинные электрические линии.

Рис. 2.43

Уравнение звена

(2.56)
где t — запаздывание сигнала во времени

Функцию можно разложить в ряд Тейлора по степеням t, полагая t малой постоянной величиной и введя замену

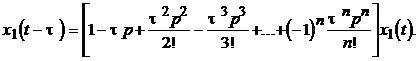(2.57)

Сравнивая это выражение с известным рядом

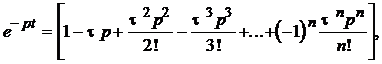(2.58)

можно записать (2.56) в операторном виде

(2.59)

Таким образом, передаточная функция запаздывающего звена представляет собой трансцендентную функцию

(2.60)

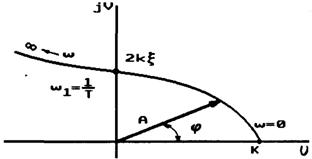
Амплитудно-фазовая частотная характеристика

  (2.61)
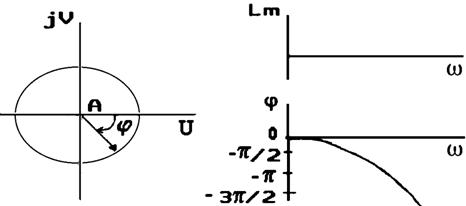
представляет собой окружность единичного радиуса (рис.2.44,а).

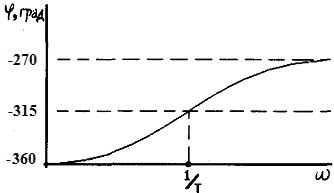
Амплитудно-частотная характеристика не зависит от частоты, а фазово-частотная характеристика пропорциональна частоте:

град.

Следует отметить, что при построении ЛФЧХ необходимо переводить радианную меру в градусную.

ЛАЧХ и ЛФЧХ этого звена приведены на рис.2.44.б. Мы рассмотрели основные типовые звенья, которые входят в состав различных САУ. Знание ЛЧХ типовых звеньев необходимо при построении ЛЧХ систем также, как знание таблицы умножения — при выполнении арифметических действий.

В практике при построении ЛЧХ САУ обычно используют шаблоны ЛЧХ типовых звеньев, приведенные в литературе.

Рис. 2.44