Теория автоматического управления. Лекция 3: Математическое описание автоматических систем управления
- Теория автоматического управления. Лекция 3: Математическое описание автоматических систем управления
- 2.2. ЛИНЕАРИЗАЦИЯ
- 2.3. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ЕГО ОСНОВНЫЕ СВОЙСТВА
- 2.4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗВЕНА
- 2.5.ТИПОВЫЕ ВОЗДЕЙСТВИЯ
- 2.6. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ САУ
- 2.7. ТИПОВЫЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ
- Элементарные неминимально-фазовые звенья
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ К ГЛАВЕ 2
Для анализа и синтеза САУ необходимо располагать ее математическим описанием — описанием физических процессов в САУ и ее основных подсистемах на языке математики. Для описания систему разбивают на отдельные подсистемы, узлы, элементы и т. д. Затем для каждого элемента составляют уравнения на основании физического закона, которому подчиняются процессы, протекающие в данном элементе. Совокупность уравнений всех элементов составляет математическое описание САУ (математическую модель САУ). Понятие математической модели связано с принятыми допущениями при составлении уравнений. Математическая модель системы должна быть, с одной стороны, как можно точнее, а с другой — по возможности проще, чтобы не усложнять исследования. Эти требования противоречивы, и только в результате разумного компромисса между ними находится математическая модель системы.
Уравнения переходных режимов называют уравнениями динамики, а уравнения установившихся режимов — уравнениями статики. Уравнения динамики — дифференциальные и интегродифференциальные, а уравнения статики — алгебраические.
Система управления и каждый ее элемент производят преобразование входной величины х(t) в выходную величину у(t). С математической точки зрения она осуществляет отображение
согласно которому каждому элементу x(t) из множества X входных сигналов ![]() ставится в соответствие единственный, вполне определенный элемент у(t) из множества Y выходных сигналов
ставится в соответствие единственный, вполне определенный элемент у(t) из множества Y выходных сигналов ![]() . Оператор A, определяющий соответствие между входными и выходными сигналами системы управления (элемента), называют оператором этой системы (элемента). Задать оператор системы — значит задать правила определения выходного сигнала системы по ее входному сигналу.
. Оператор A, определяющий соответствие между входными и выходными сигналами системы управления (элемента), называют оператором этой системы (элемента). Задать оператор системы — значит задать правила определения выходного сигнала системы по ее входному сигналу.
Все реальные системы состоят из различных элементов — механических,
электрических, электронных, гидравлических и других устройств, которые могут отличаться друг от друга по своему физическому и конструктивному выполнению. Однако, несмотря на это, многие элементы САУ описываются одинаковыми дифференциальными уравнениями, они обладают одинаковыми динамическими свойствами. Поэтому при исследовании САУ элементы делят не по физической природе и конструктивному исполнению, а по их динамическим свойствам. Этим лишний раз
подтверждается известное положение В.И.Ленина, что "единство природы обнаруживается в "поразительной аналогичности" дифференциальных уравнений, относящихся к разным областям явлений". В теории САУ элементы, процессы в которых описываются дифференциальными уравнениями не выше второго порядка, называются звеньями системы. Состояние уравнения динамики каждого конкретного звена является предметом соответствующей конкретной области технических наук (электротехники, теплотехники, динамики полета и т.п.), к которым и следует обращаться в случае необходимости.
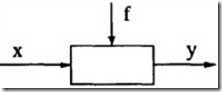
В общем случае звенья и системы описываются нелинейными дифференциальными уравнениями. Для примера рассмотрим звено (рис.2.1), которое можно описать дифференциальными уравнениями второго порядка
|
Рис. 2.1. |
где у - выходная величина, х и f - входные величины, y’ и x’ - первые производные по времени, у” - вторая производная по времени.
Уравнение (2.1), описывающее процессы в звене при произвольных входных воздействиях, называют уравнением динамики Пусть при постоянных входных величинах ![]() и
и ![]() процесс в звене с течением времени установится; величина у примет постоянное значение
процесс в звене с течением времени установится; величина у примет постоянное значение ![]() . Тогда (2.1) примет вид
. Тогда (2.1) примет вид
F(y0,0,0,x0,0)+f0=0.
Это уравнение описывает статический или установившийся режим и его называют уравнением статики .
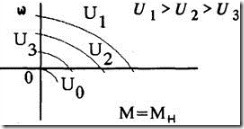
Статический режим можно описать графически с помощью статических характеристик. Статической характеристикой звена с одним входом и выходом называют зависимость выходной величины от входной в установившемся режиме. Если звено имеет несколько входов, то оно описывается с помощью семейства статических характеристик, представляющих собой кривые зависимости выходной величины у от одной величины х (или f) при различных фиксированных значениях другой — f (или х).
|
Рис. 2.2. |
Пример. В электрическом двигателе любого типа скорость вращения в установившемся режиме w является функцией двух переменных: подводимого напряжения U и момента нагрузки на валу w =f (U, Mн).
Эта зависимость представляется семеймеханических характеристикw = f1 (Мн) при фиксированных значениях управляющего напряжения const
- Prev
- Вперёд >>