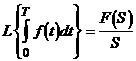Теория автоматического управления. Лекция 3: Математическое описание автоматических систем управления
- Теория автоматического управления. Лекция 3: Математическое описание автоматических систем управления
- 2.2. ЛИНЕАРИЗАЦИЯ
- 2.3. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ЕГО ОСНОВНЫЕ СВОЙСТВА
- 2.4. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЗВЕНА
- 2.5.ТИПОВЫЕ ВОЗДЕЙСТВИЯ
- 2.6. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ САУ
- 2.7. ТИПОВЫЕ ЗВЕНЬЯ И ИХ ХАРАКТЕРИСТИКИ
- Элементарные неминимально-фазовые звенья
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ К ГЛАВЕ 2
2.3. Преобразование Лапласа и его основные свойства
В ТАУ в качестве математического аппарата для анализа линейных уравнений движения систем выступает операторное преобразование Лапласа. По образному выражению академика "операционное исчисление является азбукой современной автоматики и телемеханики".
Рассмотрим функцию f (t) вещественной переменной (t), отвечающую следующим условиям:
(t) непрерывна для всех значений ³ 0, допускается конечное число точек разрыва непрерывности первого рода
3) f (t) имеет ограниченный порядок возрастания, т.е. можно указать такие постоянные числа 0 и С0 ³ 0, при которых выполняется неравенство
![]() ,
,
где число С0 является показателем роста функции
Функция f (t), удовлетворяющая условиям (1) — (3), называется оригиналом.
Пример: 1(t), 1(t)Asinwt, eat 1(t), t n 1(t). Изображением функции f (t) по Лапласу называется функция F(S) комплексного переменного S=с+jw, определяемая равенством
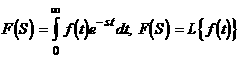 , (2.14)
, (2.14)
где L - оператор Лапласа.
Рассмотрим основные свойства преобразования Лапласа.
1. Свойство линейности:
2. Дифференцирование оригинала:
Если начальные условия нулевые, т.е.
то последняя формула принимает вид
![]() ,
,
т.е. дифференцированию f(t) соответствует умножение изображения F(S) на S.
3. Интегрирование оригинала:
При нулевых начальных условиях интегрирование оригинала сводится к делению изображения на S:
Свойства 3 и 2 позволяют дифференциальные и интегральные уравнения преобразовать в алгебраические, что существенно упрощает исследование САУ.
4. Теорема запаздывания. Для любого положительного числа t
5. Теорема о свертке (теорема умножения изображений)
Если f1(t) и f2(t) — оригиналы, а F1(S) и F2(S) — ихизображения, то
Интеграл правой части называют сверткой функции f1(t) и f(t) и обозначают f1(t)*f2(t).
6. Теорема о предельных значениях.
Если f(t) оригинал, а F(S) — его изображение, то
![]() , и при существовании предела
, и при существовании предела![]() ,
,