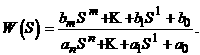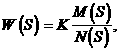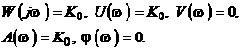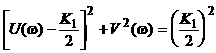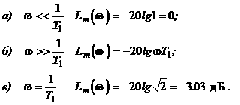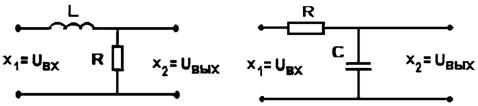Лекции для студентов

Теория автоматического управления. Лекция 3: Математическое описание автоматических систем управления

2.7. Типовые звенья и их характеристики

Типовыми называют динамические звенья, описываемые дифференциальными уравнениями не выше второго порядка. Основные типы звеньев делят на три группы: позиционные, дифференцирующие и интегрирующие.

Позиционными называют звенья, выходная и входная величины которых связаны пропорциональной зависимостью в установившемся режиме.

В общем случае передаточная функция такого звена имеет вид

(2.32)

Передаточную функцию типового звена обычно приводят к стандартному виду (свободные члены полиномов равны l):

(2.33)
где

Интегрирующими называют звенья, выходную и входную величины которых в установившемся режиме связывает интегральная зависимость.

Если в выражении (2.17) коэффициент а₀=0, то передаточная функция W(S) имеет вид

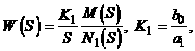(2.34)
где N₁(S) имеет свободный член, равный 1.

Передаточная функция W(S) содержит одно интегрирующее звено (сомножитель знаменателя S имеет первую степень). У дифференцирующих звеньев в выражении (2.32) отсутствует свободный член числителя, т.е. для однократно дифференцирующего звена будет

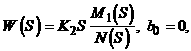(2.35)
где М₁( S) имеет свободный член, равный 1;

Интегрирующие и дифференцирующие звенья более высоких порядков получают из (2.32) в случае равенства 0 коэффициентов более высоких порядков соответственно знаменателя и числителя передаточной функции.

Знание характеристик типовых звеньев столь же необходимо для расчетов систем управления, как знание таблицы умножения в арифметике.

2.7.1. Позиционные звенья

Идеальное пропорциональное (безынерционное) звено

К таким звеньям относятся элементы САУ, инерция которых пренебрежительно мала по сравнению с инерцией всей системы. К таким звеньям электромеханических систем можно отнести рычажную механическую передачу, ламповые и транзисторные усилители, потенциометрические датчики и т.п.

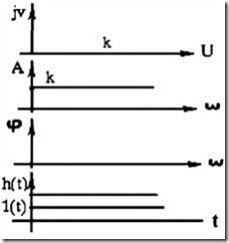
Уравнения и передаточная функция звена

Рис. 2.15

Амплитудно-фазовая характеристика (рис.2.15);

ЛАХ имеет вид

Поскольку АЧХ A(w) не зависит от частоты, то и ЛАХ представляет собой прямую линию, проведенную параллельно оси абсцисс на высоте, равной ординате (дБ).

Переходная функция

Импульсно-переходная функция

Инерционное (апериодическое) звено первого порядка

 Уравнение и передаточная функция звена

.

Частотная передаточная функция (АФХ)

.

Умножив числитель и знаменатель на комплексно-сопряженную знаменателю функцию, получим

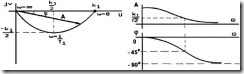
Вещественная частотная ВЧХ U(w) и мнимая V(w) МЧХ частотная характеристики:

, .

Амплитудная АЧХ и фазовая ФЧХ частотные характеристики (рис.2.16,б):

(2.36)

(2.37) 

АФХ (рис.2.16,а) представляет собой полуокружность для частот . Действительно, .

Сравнивая выражения U(w) и A(w), видим, что
Тогда

.

представляет собой уравнение окружности при изменении частоты -¥ £ w £ +¥.

Радиус этой окружности , центр ее располагается по положительной оси U(w) на удалении.

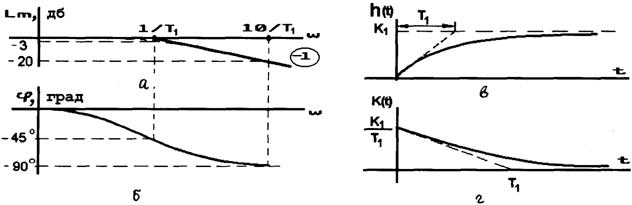
а б Рис. 2.16. Логарифмическая амплитудная частотная характеристика (рис.2.17,а)

.

Для построения ЛАХ примем К₁= 1 и рассмотрим три участка ЛАХ:

В области высоких частот при ЛАХ является линейной функцией логарифма частоты и обращается в нуль, т.е. сопрягается с выражением L_m(w) в области низких частот при частоте , называемой сопрягающей частотой. Если увеличить частоту w в 10 раз, , то получим

Таким образом, в области высоких частот ЛАХ апериодического звена представляется прямой линией с наклоном -20дБ/дек.

В дальнейшем наклоны ± 20дБ/дек, ± 40дБ/дек будем обозначать соответственно ±1, ±2.

Наибольшее отличие асимптотической ЛАХ от точной будет на частоте сопряжения , равно -3 дБ.

Если коэффициент К₁ апериодического звена не равен 1 (), то при ЛАХ смещается параллельно вверх на величину 20 lg, а при - вниз вдоль оси ординат на . 

Рис. 2.17

Переходная функция, согласно решению уравнения звена, при и нулевых начальных условиях представляет собой экспоненту (рис.2.17.в) и описывается выражением

.

Импульсно-переходная (весовая) функция (рис.2.1.г)

.

Примером апериодического звена могут быть: электродвигатель постоянного тока (в первом приближении), если - управляющее напряжение, — угловая скорость вала двигателя; сглаживающие L-R и R-С — фильтры (рис.2.18).

Рис. 2.18

Инерционное звено второго порядка

Вид дифференциального уравнения

, ,

, .

Передаточная функция

.

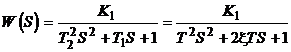При выполнении условия

корни характеристического уравнения

,
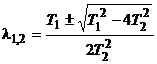
будут вещественными.

В этом случае инерционное звено 2-го порядка называют апериодическим звеном 2-го порядка. Его передаточная функция

,

Рис. 2.19, а

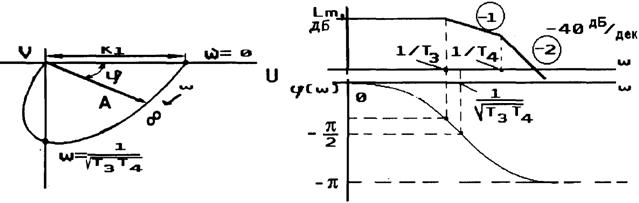
Переходная характеристика (рис.2.19,а)

где

АФЧХ (рис.2.19,б)

АЧХ

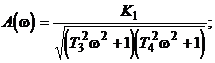
ФЧХ (рис.2.20)

 

 ЛАХ (рис.2.20)

Рис. 2.19, б Рис. 2.20

Если , то частоты сопряжения сходятся в одну точку.

Примером такого звена является двигатель постоянного тока при учете инерционности цепи якоря, электромашинный усилитель.

Если выполняется условие , то корни характеристического

уравнения - комплексные.

 

 Инерционное звено 2-го порядка с передаточной функцией

называется колебательным;

 — параметр затухания (коэффициент относительного демпфирования).

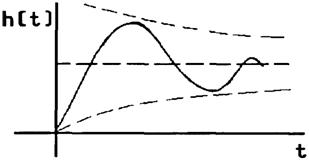
Переходная характеристика (рис.2.21)

  

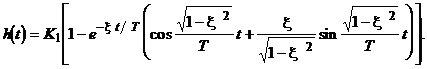
Рис. 2.21

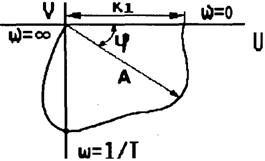
Амплитудно-фазовая характеристика (рис.2.22);

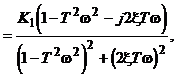(2.39)

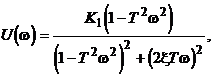
Рис. 2.22

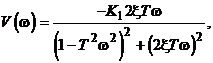
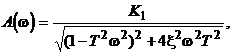(2.40)

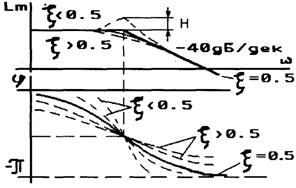
ЛАХ и ФЧХ (рис.2.23):

(2.41)

1)

Рис.2.23

2)

Пусть , , следовательно а

При

При

3) 

Таким образом, асимптотическая ЛАЧХ в области низких частот параллельна оси частот, а при имеет наклон "-2", т.е. -40 дБ/дек.

При значениях характеристика близка к ломаной. Если же , то получится заметный горб (резонансный пик). Имеются шаблоны для вычерчивания точной ЛАХ. В упрощенных расчетах достаточно находить величину резонансного пика на частоте сопряжения:

Примерная последовательность действий при построении ЛЧХ звена 2-го порядка

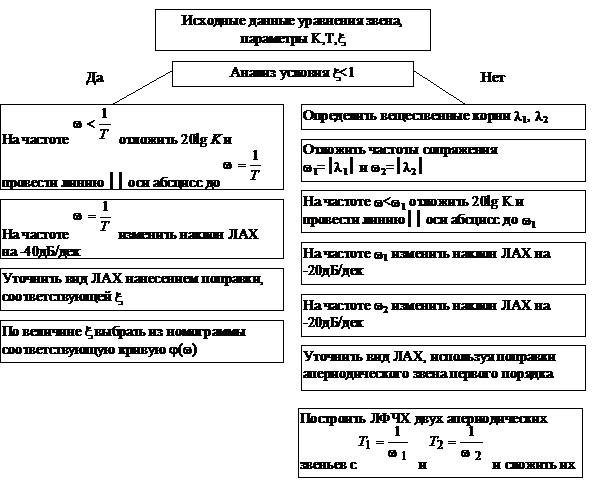
Консервативное звено

В частном случае ( = О) колебательное звено вырождается в консервативное звено с передаточной функцией

Частотная передаточная функция

(2.42)

АЧХ

(2.43)

При АЧХ претерпевает разрыв ФЧХ, как это следует из годографа (рис.2.24,а), АФХ имеет вид

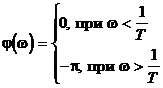(2.24)

Переходная функция  

В установившемся режиме в консервативном звене возникают незатухающие гар­монические колебания (рис.2.24,б).

ЛАХ (рис.2.25) на частоте также имеет разрыв.

Неустойчивые (неминимально-фазовые) звенья

При рассмотрении инерционных звеньев первого и второго порядков было показано, что переходные характеристики изменялись по затухающему апериодическому или колебательному закону. Это обусловлено тем, что характеристические уравнения этих звеньев не имели вещественных положительных корней или комплексных корней с положительной вещественной частью. Особенностью этих звеньев является наличие минимального фазового сдвига, характеризуемого ФЧХ .

Однако существуют звенья, у которых корни характеристических уравнений имеют положительные вещественные части. Переходные характеристики таких звеньев имеют расходящийся характер, такие звенья являются неустойчивыми и имеют следующие передаточные функции:

,

, (2.45)

Характеристическое уравнение неустойчивого апериодического звена имеет положительный вещественный корень:

Рис. 2.26

 

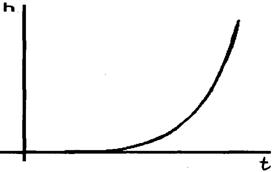
Переходная характеристика (рис.2.26) имеет апериодический расходящийся вид. Частотные характеристики такого звена:

.

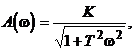
Сравнивая это выражение с выражением для апериодического устойчивого звена, видим, что АЧХ звеньев совпадают, а фазовый сдвиг во втором случае значительно больше. Эта особенность характерна для всех звеньев (2.45). Поэтому неустойчивые звенья относятся к так называемым неминимально-фазовым звеньям. По аналогии САУ, содержащие такие звенья, называют неминимально-фазовыми системами.

В минимально-фазовых системах существует аналитическая зависимость между АЧХ и ФЧХ. Благодаря этой зависимости можно по АЧХ минимально-фазовой САУ (звена) определить фазовый сдвиг на некоторой частоте по формуле Н.Винера

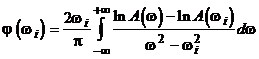(2.47)
где  выражено в радианах.

Для ЛЧХ фазовый сдвиг в минимально-фазовых САУ определяется наклоном асимптотической ЛАХ вблизи рассматриваемой частоты .

Следует понять и запомнить следующее:

если ЛАХ параллельна оси абсцисс, то при

если ЛАХ представляет собой прямую с наклоном ±20дБ/дек, то±90°;а при наклоне ±40дБ/дек при.

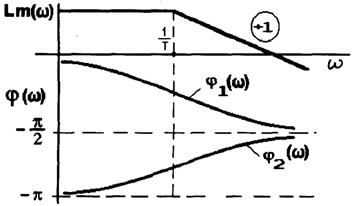
Рис. 2.27

В неминимально-фазовых системах (звеньях) такая аналитическая зависимость между АЧХ и ФЧХ отсутствует, при этом фазовый сдвиг будет больше в неминимально-фазовой системе. На рис.2.27 приведены ЛЧХ устойчивого и неустойчивого апериодических звеньев. Из рис.2.27 видно, что ФЧХ в области низких частот имеет значительно большее по модулю значение, чем ФЧХ устойчивого звена. В неминимально-фазовых САУ труднее компенсировать фазовые сдвиги, чем в минимально-фазовых, поэтому такие системы имеют относительно худшие показатели качества.

Основные сведения об элементарных неминимально-фазовых звеньях приведены в табл. 2.1. ЛАХ этих звеньев строится аналогично ЛАХ соответствующих минимально- фазовых звеньев. Также следует учитывать, что некоторые полиномы второго порядка с правым корнем могут быть разложены на произведение полиномов первой степени, например: