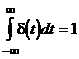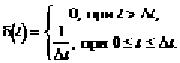Лекции для студентов

Теория автоматического управления. Лекция 3: Математическое описание автоматических систем управления

2.5.Типовые воздействия

САУ функционирует под действием управляющих и возмущающих сигналов. По отношению к указанным воздействиям САУ должна вести себя по-разному. В соответст­вии с управляющим сигналом происходит изменение регулируемых переменных, возмущающие же воздействия должны как можно меньше влиять на изменение регулируемых переменных.

Для правильного проектирования САУ или даже для составления технических тре­бований к ней необходимо знать условия ее работы, т.е. знать возмущения, действующие на систему. Прикладываемые к САУ воздействия отличаются крайним разнообразием. Поэтому для анализа и синтеза САУ приняты наиболее часто встречающиеся или небла­гоприятные стандартные или типовые воздействия, которые задают в виде функций времени. Реакция системы на стандартные возмущения характеризует основные динами­ческие свойства САУ.

Для всех САУ в качестве типовых воздействий обычно используют следующие сигна­лы:

1. Ступенчатый сигнал в виде единичной функции 1(t) - ступенчатый скачок (рис.2.5.)

Рис. 2.5

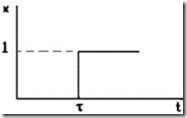
Если действие единичного сигнала проявляется со смещением во времени т после момента t = 0 (рис.2.6), то соответствующая функция имеет вид

Рис. 2.6.

2. Сигнал в виде импульсной функции первого порядка или d (t) — функции.

Импульсная функция представляет собой импульс бесконечно малой длительности. Математически он описывается функцией d (t) (дельта‑функция), которую можно пред­ставить как производную от единичной функции в момент t=0:

Отсюда следует

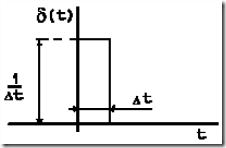
Таким образом, площадь импульса имеет конечную величину, равную 1. Импульсная d — функция может рассматриваться как ударное воздействие с продол­жительностью значительно меньшей длительности переходного процесса. В этом случае величина импульса будет (рис. 2.7).

Рис. 2.7.

3. Гармонический входной сигнал задается в виде функции

х(t)=А sin w t,
где А - амплитуда колебаний, часто принимают A=1,

 — круговая частота колебаний;

Т - период колебаний.

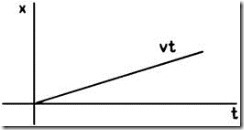
4. Линейно возрастающий сигнал х(t)=Vt при t ³ 0. Согласно этому входное воздействие должно изменяться с постоянной скоростью (рис. 2.8).

Рис. 2.8.

5. Степенные функции времени:

квадратичная ;

кубическая .

Для задания сигналов в виде ступенчатой, импульсной и гармонической функции применяют генераторы импульсов и периодических колебаний.

• << Назад
• Вперёд >>