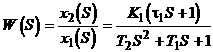Лекции для студентов

Теория автоматического управления. Лекция 3: Математическое описание автоматических систем управления

2.4. Передаточная функция звена

Ее определение дается на основе преобразования Лапласа. Рассмотрим динамическое звено (рис.2.4), описываемое дифференциальным уравнением

Рис. 2.4

. (2.22)

Или в символической записи

с начальными условиями:

Тогда

Применив преобразование Лапласа к уравнению (2.22), получим

, (2.23)

где через B(S) обозначен многочлен, включающий в себя все члены с величинами начальных условий.

При нулевых начальных условиях В(S) =0.

В этом случае динамические свойства звена характеризуются передаточной функ­цией 

, (2.24)

Определение. Передаточной функцией звена W(S) называется отношение изображений Лапласа выходной и входной величин при нулевых начальных условиях.

В общем случае уравнение звена или последовательности звеньев, после исключения промежуточных переменных, можно представить в виде

(2.25)
где x_вх (t) — входная величина; x_вых (t) — выходная величина.

Правая часть уравнения (2.25) характеризует воздействие, поданное на вход. Левая часть, приравненная к нулю, характеризует свойства самого звена, его свободное движение. Порядок уравнения определяет число степеней свободы звена.

Формально передаточную функцию звена можно составить как отношение опера­торных многочленов левой и правой частей уравнения звена и, наоборот, зная передаточ­ную функцию, легко написать уравнение звена.

Передаточная функция W (S) имеет вид дробно-рациональной функции от перемен­ной:

(2.26)

Для физически реализуемых звеньев выполняется условие n ³ m. 

Следует отметить, что при ненулевых начальных условиях передаточные функции неполно описывают процессы в звеньях и системах. Если собственный оператор N(S) и оператор воздействия М(S) имеют общие множители, то они при вычислении w (S) сокращаются.

И в этом случае по передаточной функции системы нельзя восстановить ее диффе­ренциальное уравнение и получить описание процессов в ней при произвольных началь­ных условиях.

Корни уравнения М(S)=0 называют нулями передаточной функции, а корни уравне­ния N(S) =0 — полюсами.

Коэффициенты a_i ( i=0 , ... , п) и b_j ( j=0 , ... , т ) вещественны, так как они явля­ются функциями параметров системы.

• << Назад
• Вперёд >>