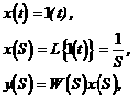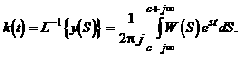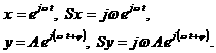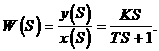Лекции для студентов

Теория автоматического управления. Лекция 3: Математическое описание автоматических систем управления

Страница 6 из 9

2.6. Основные характеристики САУ

Характеристики САУ делят на временные и частотные.

2.6.1. Временные характеристики

1. Переходная функция

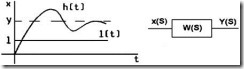
Переходной функцией h(t) называют реакцию звена или системы на единичное ступенчатое воздействие 1(t) на входе при нулевых начальных условиях:

откуда

(2.27)

Рис. 2.9.

2. Импульсная переходная или весовая функция

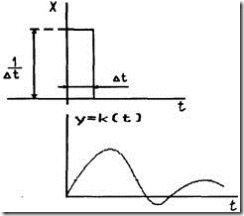
Импульсной переходной или весовой функцией звена (системы) называют реакцию звена (системы) на единичное импульсное воздействие при нулевых начальных условиях (рис.2. 10).

Импульсная переходная функция представляет собой оригинал (обратное преобразование Лапласа передаточной функции). Зная импульсную переходную функцию k(t), можно определить передаточную функцию звена (системы):

Рис 2.10.

(2.28)

2.6.2. Частотные характеристики

Частотными характеристиками называют формулы и графики, характеризующие реакцию звена на гармоническое входное воздействие в установившемся режиме, т.е. вынужденные гармонические колебания звена.

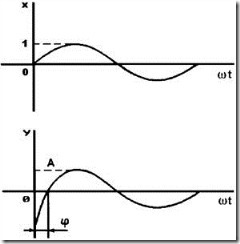
Если на вход звена подается единичный синусоидальный сигнал (рис.2.11)

х(t)=sin wt,

то на выходе будет (в установившемся режиме)

у(t)=А sin (wt+j),

где А - амплитуда (усиление амплитуды);

j — сдвиг фазы относительно входного сигнала.

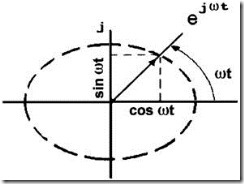
Применяется символическая запись синусоидальных колебаний в виде (строго говоря, е^j^w^t=cos wt + j sin wt), что геометрически изображается вращающимся единичным вектором (рис.2.12). Проекции последнего на прямоугольные оси дают cos wt и sin wt. Поэтому для суждения о вынужденных синусоидальных колебаниях звена достаточно исследовать реакцию звена на сигнал е^j^w^t.

Рис. 2.11

Рис. 2.12

Пусть уравнение звена имеет вид

(TS+1)y=KSx. (2.29)

Используем символическую запись:

Подставив эти величины в уравнение звена, получим

откуда

Сравним эти выражения с передаточной функцией звена:

(2.30)

Из сопоставления видно, что

(2.31)

Функцию W(jw) называют частотной передаточной функцией или амплитудно — фазовой частотной передаточной характеристикой (АФХ). Функцию А(w) - амплитудно — частотной характеристикой (АЧХ). Функцию j(w)‑фазовой частотной характеристикой (ФЧХ).

Кроме показательной формы, W(jw) можно представить и в алгебраической:

W(jw)=U(w)+jV(w)=A(w)cos j(w)+jA(w)sin j(w),
где U(w) — вещественная частотная характеристика (ВЧХ);

V (w) — мнимая частотная характеристика (МЧХ).

Связь между частотными характеристиками. - т.е. АЧХ представляет собой модуль частотной передаточной функции и определяет, во сколько раз амплитуда выходного гармонического сигнала отличается от амплитуды входного сигнала.

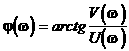— аргумент передаточной функции W(jw), определяет фазовый сдвиг между выходной и входной синусоидами.

Рис. 2.13

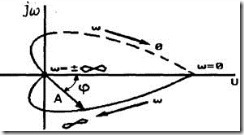
АФХ W(jw) может быть изображена как годограф на комплексной плоскости (рис.2.13) в полярных ( А,j ) либо в прямоугольных координатах ( U, V ). При этом частоту w изменяют от 0 до ¥ (сплошная кривая на рис.2. 13) или же от -¥ до ¥, когда добавляется еще симметричная к ней пунктирная кривая.

Следует отметить, что ВЧХ U(w)=А(w)cos j(w) есть четная функция частоты w, а МЧХ V(w)=А() sin j() - нечетная функция частоты. Этим и объясняется зеркальная симметрия АФХ относительно оси абсцисс.

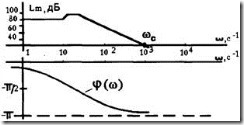
Логарифмические частотные характеристики. Ускорение и упрощение расчетов САУ достигается при использовании логарифмических амплитудно-частотных характеристик и логарифмических фазово-частотных характеристик Такое построение было предложено Боде в 1945 г. и получило дальнейшее развитие в трудах ученых и др.

При построении логарифмических частотных характеристик пользуются единицами измерений, заимствованными из других областей науки и техники. Эти единицы служат для оценки коэффициента усиления и диапазона частот. В акустике, и радиотехнике для измерения разности уровней (усиления или ослабления) звуковых или электромагнитных мощностей применяются логарифмическая шкала и безразмерные логарифмические единицы. Для этого существуют следующие основания:

1. Диапазон, в котором изменяется сила (интенсивность) звука, весьма велик: от Вт/см(слабые звуки вблизи порога слышимости) до Вт/см(громкие звуки, вызывающие болевые ощущения), т.е. изменение в раз. Во избежание столь огромных чисел используют их логарифмы и вводят логарифмический масштаб и логарифмические единицы.

Рис. 2.14

2. В соответствии с законом Вебера-Фехнера восприятие звука в известных пределах пропорционально десятичному логарифму раздражения, т.е. человеческое ухо реагирует на изменение мощности звука по закону логарифма.

Следует отметить, что А>1 соответствует верхняя полуплоскость ЛАЧХ (усиление амплитуды), A<1 (ослабление амплитуды) — нижняя полуплоскость ЛАЧХ; A=1 соответствует значение L_m=0, частота, соответствующая значению L_m=0, называется частотой среза w_c.