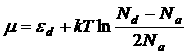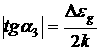Физика полупроводников. Лекция 3
- Физика полупроводников. Лекция 3
- §2. Связь уровня химического потенциала с концентрацией равновесных носителей заряда в невырожденных полупроводниках.
- §3. Концентрация равновесных носителей заряда в собственных невырожденных полупроводниках.
- §4. Концентрация равновесных носителей заряда в невырожденных полупроводниках с одним типом мелких примесных центров и низких температурах.
- §5. Концентрация равновесных носителей заряда в невырожденных полупроводниках с одним типом примесных уровней при высоких температурах.
- §6. Концентрация равновесных носителей заряда в полупроводниках с двумя типами примесных центров и их полной компенсации.
- §7. Равновесная концентрация носителей заряда в частично компенсированных невырожденных полупроводниках.
- §8. Условие перехода полупроводника в вырожденное состояние и равновесная концентрация носителей заряда в полностью вырожденном полупроводнике.
Рассмотрим общий случай, когда концентрация ![]() мелких доноров отличается от концентрации
мелких доноров отличается от концентрации ![]() мелких акцепторов. Для определенности положим, что
мелких акцепторов. Для определенности положим, что ![]() . В этом случае мелкие доноры и мелкие акцепторы в количестве
. В этом случае мелкие доноры и мелкие акцепторы в количестве ![]() будут взаимно компенсированы, т.е. все акцепторы будут заполнены электронами пришедшими с донорных центров, следовательно,
будут взаимно компенсированы, т.е. все акцепторы будут заполнены электронами пришедшими с донорных центров, следовательно, ![]() . Число некомпенсированных доноров способных участвовать в тепловой генерации электронов в с — зону будет равно:
. Число некомпенсированных доноров способных участвовать в тепловой генерации электронов в с — зону будет равно: ![]() — эффективная концентрация доноров. Значит, при соотношении
— эффективная концентрация доноров. Значит, при соотношении ![]() полупроводник ведет себя как полупроводник
полупроводник ведет себя как полупроводник ![]() — типа. В таком полупроводнике нет примесных дырок, а есть дырки образуемые в результате собственных переходов при высоких температурах. Уравнение электронейтральности для такого полупроводника с учетом предыдущего параграфа будет иметь вид:
— типа. В таком полупроводнике нет примесных дырок, а есть дырки образуемые в результате собственных переходов при высоких температурах. Уравнение электронейтральности для такого полупроводника с учетом предыдущего параграфа будет иметь вид:
Рассмотрим несколько придельных случаев.
В этом случае ![]() ,
, ![]() . Тогда уравнение электронейтральности примет вид:
. Тогда уравнение электронейтральности примет вид:
Подставим (3) в выражение для ![]() , получим:
, получим:
Видно, что энергия активации ![]() .
.
2. Низкие температуры.
В этом случае ![]() ,
, ![]() . Тогда уравнение электронейтральности примет вид:
. Тогда уравнение электронейтральности примет вид:
![]() — концентрация доноров занятых электронами.
— концентрация доноров занятых электронами.
![]() — эффективная концентрация ионизированных доноров.
— эффективная концентрация ионизированных доноров.
Такое уравнение решено в §4.
Видно, что энергия активации ![]() .
.
3. Высокие температуры.
В этом случае нельзя пренебрегать величиной ![]() ,
, ![]() . Тогда уравнение электронейтральности примет вид:
. Тогда уравнение электронейтральности примет вид:
Решение этого уравнения в §5. При высоких температурах:
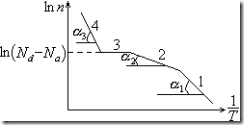
По величине ![]() , в этой области можно определить эффективную концентрацию
, в этой области можно определить эффективную концентрацию ![]() .
.
4. Очень высокие температуры.