Лекции для студентов

Физика полупроводников. Лекция 3

§6. Концентрация равновесных носителей заряда в полупроводниках с двумя типами примесных центров и их полной компенсации.

На практике чаще встречаются полупроводники, содержащие как мелкие доноры, так и мелкие акцепторы. На рисунке показана зонная схема и схема тепловых переходов в таком полупроводнике.

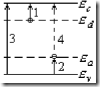При T > 0 K⁰ в таком полупроводнике могут иметь место тепловые переходы 1 — 4 приводящие к образованию электронов и дырок. Очевидно, примесные переходы 4 будут мало актуальными, потому что энергия активации для таких переходов , так как концентрация примесных атомов значительно меньше, чем собственных атомов то число переходов 4 в единицу времени будет значительно меньше, чем переходов 3, поэтому переходами 4 можно пренебречь. Запишем уравнение электронейтральности для полупроводника, имеющего мелкие доноры и акцепторы, исходя из условия, что в любом физически малом объеме полупроводника суммарный заряд всех частиц равен нулю. Будем рассматривать единичный объем кристалла. Отрицательный заряд в таком объеме создается свободными электронами с концентрацией и отрицательно заряженными акцепторами . Положительный заряд обеспечивается и . Тогда уравнение электронейтральности примет вид:

, ,

Рассмотрим такой полупроводник, у которого концентрации мелких доноров и акцепторов равны между собой: . Это условие соответствует полной компенсации донорно-акцепторных центров. Примесные электроны зоны проводимости, появившиеся за счет переходов 1, блуждая по кристаллу, встречаются с примесными дырками, появившееся за счет переходов 2 и рекомбинируют с образованием собственных атомов полупроводника. При наличии в полупроводнике мелких доноров и мелких акцепторов каналы рекомбинации и генерации носителей заряда не являются взаимообратными, как это бы имело место, если бы полупроводник содержал один тип мелких акцепторов. В этом случае рекомбинация происходит с образованием, как показано выше собственных атомов, а не их примесных центров, следовательно, за время порядка с момента нагревания полупроводника все примесные центры мелких доноров и акцепторов опустошаются, т.е. все мелкие доноры заряжаются положительно, а мелкие акцепторы отрицательно. Они перестают быть электрически активными, т.е. не являются поставщиками электронов и дырок в свои зоны, значит в этих условиях

,

Тогда уравнение электронейтральности примет вид:

,

Значит электропроводность полностью компенсированного полупроводника, является собственной электропроводностью. Число носителей заряда в таком полупроводнике будет таким же, как в чистом полупроводнике при прочих равных условиях. Однако другие физические характеристики такого полупроводника отличаются от чистого полупроводника. Полностью компенсированный полупроводник содержит два типа полностью заряженных примесных центров. Они являются эффективными рассеивателями носителей заряда. Подвижность носителей заряда в таких полупроводниках будет значительно ниже, чем подвижность в чистых полупроводниках.