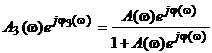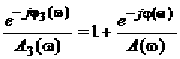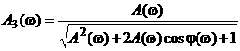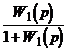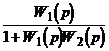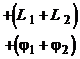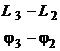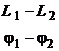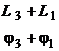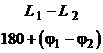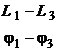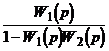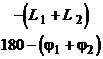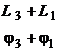Лекции для студентов

Теория автоматического управления. Лекция 4: Основные характеристики систем автоматического управления

Страница 7 из 8

3.7. Частотные характеристики замкнутой системы

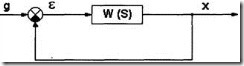
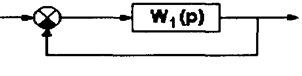
Для системы с единичной обратной связью (рис.3.15) запишем передаточную функцию замкнутой системы по управлению

Рис. 3.15

, (3.33)
причем — ПФ разомкнутой системы.

Частотные передаточные функции разомкнутой и замкнутой систем ()

,

,
где - соответственно АЧХ и ФЧХ разомкнутой и замкнутой систем. В соответствии с (3.33) можно записать:

,

.

Или подставив сюда и приравнивая затем отдельно действительные и мнимые части, получим

Сложив сначала квадраты этих выражений, а затем, поделив одно из них на другое, получим

, (3.34)

. (3.35)

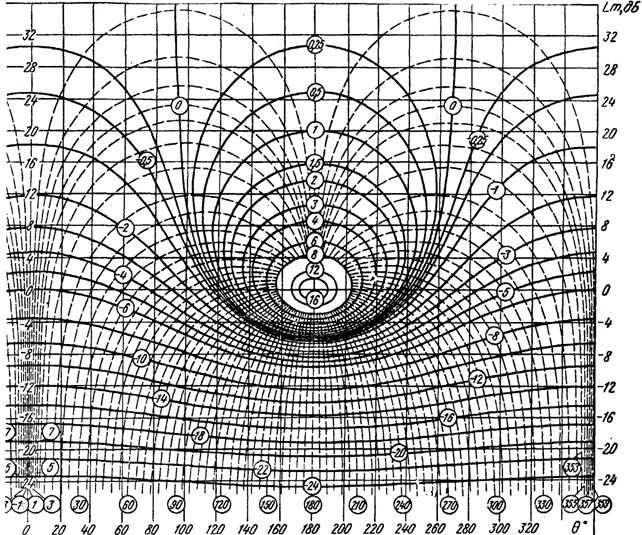
Формулы (3.34) и (3.35) являются исходными для построения номограммы замыкания (рис.3.16), позволяющими по заданным ЛЧХ разомкнутой системы [20lgA(w) и j(w)] находить ЛЧХ системы, замкнутой единичной отрицательной обратной связью .

Номограммой замыкания пользуются следующим образом. По оси абсцисс откладывают значение фазы , а по оси ординат ЛАХ для ряда фиксированных частот . Величины находят по ближайшим кривым постоянных значений модуля фазы ПФ замкнутой системы.

Таким образом, для ряда значений частот строится вся частотная характеристика замкнутой системы.

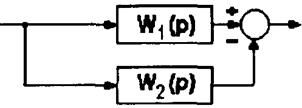
Следует отметить, что номограммами замыкания следует пользоваться лишь при значениях в пределах дБ ,так как с точностью до 1дБ имеем

при и

при .

Другими словами, в области частот, где модуль ПФ разомкнутой системы больше десяти, ЛАХ замкнутой системы совпадает с осью частот, а в области частот, где модуль ПФ разомкнутой системы меньше 0.1, ЛАХ замкнутой системы совпадает с ЛАХ разомкнутой системы.

Рис. 3.16. Номограмма для определения амплитудной и фазовой частотных характеристик замкнутой систему по амплитудно-фазовой характеристики разомкнутой системы.

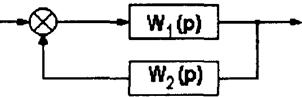
Номограмма замыкания может использоваться и для построения ЛЧХ различных соединений звеньев. Правила пользования номограммой для наиболее распространенных случаев соединения приведены в табл. 3.2, где приняты следующие обозначения:

,

— значение ЛАЧХ и ФЧХ, полученные при отсчете в криволинейных координатах замыкания.

Таблица 3.2

N п/п	Схема	Передаточная функция	Отложить на номограмме	Результат
1
2
3
4
5

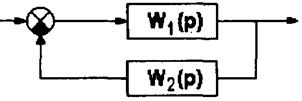
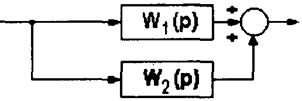
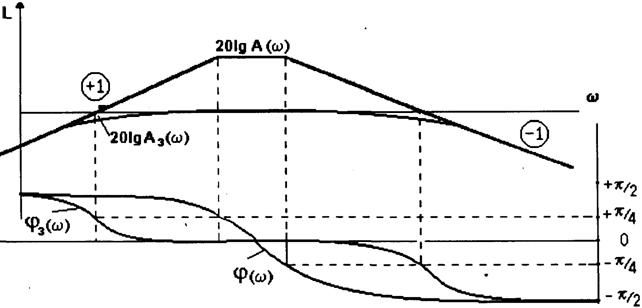
Номограмма замыкания может использоваться при построении ЛЧХ многоконтурных систем. При этом часто встречается задача построения ЛЧХ звена, охваченного местной обратной связью. Рассмотрим подробнее решение этой задачи (табл.3.2, N 2).

Рис.3.17. ЛЧХ разомкнутой и замкнутой системы

Поскольку номограмма рассчитана для систем с единичной ООС, то рассматриваемая структура преобразуется к одному из нижеследующих видов (рис.3.18).

Рис.3.18

т.е. исходная передаточная функция преобразуется к виду

. (3.36)

ЛЧХ находится по номограмме замыкания, если использовать ЛАХ и ФЧХ .

Рис.3.19

При использовании обратных передаточных функций (рис.3.19) исходная ПФ преобразуется к виду

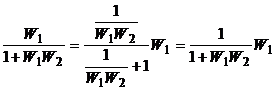. (3.37)

ЛЧХ, соответствующие передаточной функции 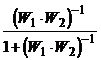находятся по номограмме замыкания при использовании обратных ЛЧХ и

В соответствии с выражениями (3.36) и (3.37) требуемые ЛЧХ получаются, если в первом случае от ЛАХ и ФЧХ 201g и отнять ЛАХ 201g и ФЧХ звена обратной связи.