Лекции для студентов

Теория автоматического управления. Лекция 4: Основные характеристики систем автоматического управления

Страница 5 из 8

3.5. Передаточные функции и уравнения замкнутой системы

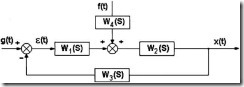
Рассмотрим определение передаточных функций (ПФ) замкнутой системы (рис.3.14) при известных передаточных функциях всех звеньев САУ.

Рис.3.14. Структурная схема одноконтурной системы:

g(t) — задающее воздействие; f(t) — возмущающее воздействие: x(t) — регулируемая (выходная) переменная: e(t)- ошибка (рассогласование) замкнутой САУ

Согласно структурной схеме можно записать:

, (3.18)

. (3.19)

Уравнение (3.19) называют обычно уравнением замыкания.

Подставляя в уравнение (3.18) значение ошибки из (3.19), после несложных преобразований получим:

; (3.20)

передаточную функцию разомкнутой системы

; (3.21)

передаточную функцию замкнутой системы по управлению

; (3.22)

передаточную функцию замкнутой системы по возмущению

. (3..23)

Теперь в выражение (3.19) подставим X(S) из (3.18).

Решая уравнение относительно , получим уравнение ошибки замкнутой системы

. (3.24)

В выражении (3.24) можно выделить две передаточные функции:

а) передаточную функцию ошибки замкнутой системы от задающего воздействия g(t)

; (3.25)

б) передаточную функцию ошибки замкнутой системы от возмущающего воздействия

. (3.26)

Важно отметить, что все передаточные функции замкнутой системы имеют один и тот же знаменатель и отличаются только числителем.

Дифференциальное уравнение замкнутой системы можно получить из (3.20) или (3.24) умножением всего выражения на знаменатель и, переходя к оригиналам, в символической форме получим:

(3.27)