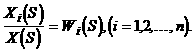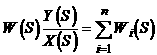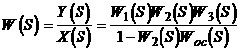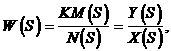Теория автоматического управления. Лекция 4: Основные характеристики систем автоматического управления
- Теория автоматического управления. Лекция 4: Основные характеристики систем автоматического управления
- 3.2. ПОСТРОЕНИЕ ЛЧХ РАЗОМКНУТОЙ ОДНОКОНТУРНОЙ СИСТЕМЫ
- 3.3. СОСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ САУ
- 3.4. ПРАВИЛА ПРЕОБРАЗОВАНИЯ СТРУКТУРНЫХ СХЕМ
- 3.5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И УРАВНЕНИЯ ЗАМКНУТОЙ СИСТЕМЫ
- 3.6. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ
- 3.7. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТОЙ СИСТЕМЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ К ГЛАВЕ 3
Глава 3. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
3.1. Передаточные функции разомкнутой системы
В зависимости от способа получения требуемых характеристик и технической реализации звенья могут быть соединены в различные комбинации. Структурная схема представляет собой графическое отображение математической модели Как бы сложна ни была структурная схема в ней всегда можно выделить три типовых соединения однонаправленных звеньев: последовательное; параллельное; параллельное.
Однонаправленные звенья отличаются тем, что в результате присоединения последующего звена к выходу предыдущего у последнего значение выходной координаты не изменяется. Воздействие в таких звеньях передается только в одном направлении. Найдем передаточные функции типовых звеньев.
Последовательное соединение. Рассмотрим цепочку, состоящую из последовательно соединенных однонаправленных звеньев
|
Рис. 3.1 |
Произведя последовательную подстановку, получим
Таким образом, передаточная функция цепи последовательно соединенных звеньев равна произведению передаточных функций всех звеньев.
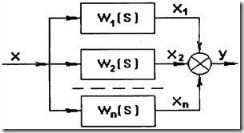
Параллельное соединение звеньев. Рассмотрим цепь, состоящую из параллельно соединенных однонаправленных звеньев
|
Рис. 3.2 |
Передаточные функции звеньев:
Выходная величина цепи равна сумме входных величин звеньев 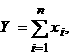 , а передаточная функция цепи имеет вид
, а передаточная функция цепи имеет вид
Следовательно, при параллельном соединении звеньев передаточная функция цепи равна сумме передаточных функций всех звеньев.
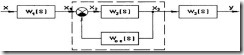
Встречно-параллельное соединение звеньев (цепь с местной обратной связью) Рассмотрим часто встречающийся случай (рис.3.3), когда одно или несколько последовательно соединенных звеньев охвачены обратной связью (положительной или отрицательной).
|
Рис. 3.3 |
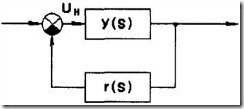
На показаны три последовательно соединенных звена. Второе звено с передаточной функцией ![]() охвачено обратной связью, которая может быть положительной или отрицательной. Рассмотрим вначале передаточную функцию звена, охваченного отрицательной обратной связью (часть схемы на обведенная пунктиром)
охвачено обратной связью, которая может быть положительной или отрицательной. Рассмотрим вначале передаточную функцию звена, охваченного отрицательной обратной связью (часть схемы на обведенная пунктиром)
При отрицательной обратной связи (ООС) для величины ![]() можно записать:
можно записать:
Для выходной величины второго звена запишем:
Отсюда получим
Передаточная функция всей схемы (рис.3.3)
Правило. Передаточная функция разомкнутой цепи с местной отрицательной (положительной) обратной связью равна произведению передаточных функций всех звеньев прямой цепи, деленному на единицу плюс (минус) произведение передаточной функции обратной связи на передаточную функцию охватываемого ею звена.
Если в той же схеме (рис. 3.3) местная обратная связь будет положительной (ПОС), то
![]()
и, рассуждая аналогично предыдущему, получим
· Обращаем ваше внимание на знак при втором слагаемом знаменателя. При ООС он положителен, а при ПОС — отрицателен.
Пользуясь выражениями 3.1), (3.2), (3.4), (3.5), можно составить общие передаточные функции для цепей различной сложности.
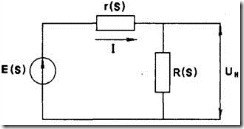
В качестве примера рассмотрим случай, где условие однонаправленности не выполняется. Примером может служить подключение к зажимам источника питания пассивной электрической цепи ( потребителя) соизмеряемой мощности (рис.3.4).
|
Рис. 3.4 |
Источник питания представлен в виде источника напряженияс внутренним сопротивлением ![]() , потребитель полным сопротивлением
, потребитель полным сопротивлением![]() .
.
Ток в цепи определяется согласно закону Ома для полной цепи
|
Рис. 3.5 |
Если сопоставить выражение (3.6) с выражением (3.3), то присоединение потребителя к источнику питания соизмеримой мощности можно представить как охват проводимости нагрузки отрицательной обратной связью через внутреннее сопротивление потребителя энергии
где M(S) и N(S) - полином числителя и знаменателя со свободными членами, равными единице; К - коэффициент передачи разомкнутой системы.
В реальных системах степень п знаменателя N(S) больше степени т числителя KM(S), т.е. п>т .
Дифференциальное уравнение разомкнутой системы в символической форме (![]() )
)
N(p)Y(t)=KM(p)x(t),
характеристическое уравнение![]() .
.
- Prev
- Вперёд >>
- Prev
- Вперёд >>