Теория автоматического управления. Лекция 4: Основные характеристики систем автоматического управления
- Теория автоматического управления. Лекция 4: Основные характеристики систем автоматического управления
- 3.2. ПОСТРОЕНИЕ ЛЧХ РАЗОМКНУТОЙ ОДНОКОНТУРНОЙ СИСТЕМЫ
- 3.3. СОСТАВЛЕНИЕ И ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ САУ
- 3.4. ПРАВИЛА ПРЕОБРАЗОВАНИЯ СТРУКТУРНЫХ СХЕМ
- 3.5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И УРАВНЕНИЯ ЗАМКНУТОЙ СИСТЕМЫ
- 3.6. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ
- 3.7. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТОЙ СИСТЕМЫ
- КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАЧИ К ГЛАВЕ 3
Рассматривая структурную схему CAP как один из видов графа, можно передаточную функцию сложной многоконтурной системы определить, не приводя ее к одноконтурному виду, с помощью формулы Мезона (Мейсона):
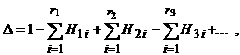 (3.32)
(3.32)
где ![]() - передаточная функция разомкнутой цепи i -го замкнутого контура структурной схемы;
- передаточная функция разомкнутой цепи i -го замкнутого контура структурной схемы;
![]() - число замкнутых контуров в схеме;
- число замкнутых контуров в схеме;
![]() — произведение ПФ разомкнутых цепей i -и пары несоприкасающихся замкнутых контуров;
— произведение ПФ разомкнутых цепей i -и пары несоприкасающихся замкнутых контуров;
![]() - число пар несоприкасающихся контуров;
- число пар несоприкасающихся контуров;
![]() - произведение ПФ разомкнутых цепей i -и тройки несоприкасающихся контуров;
- произведение ПФ разомкнутых цепей i -и тройки несоприкасающихся контуров;
![]() - число троек несоприкасающихся контуров;
- число троек несоприкасающихся контуров;
![]() — ПФ 1-й прямой цепи от переменной х к переменной у;
— ПФ 1-й прямой цепи от переменной х к переменной у;
r - число прямых цепей от х к у;
![]() - функция
- функция ![]() для той части структурной схемы, которая не соприкасается с i -и прямой цепью от х к у.
для той части структурной схемы, которая не соприкасается с i -и прямой цепью от х к у.
Используя формулу (3.31), нужно иметь в виду следующее:
1. Прямые цепи от х к у могут частично совпадать одна с другой.
2. При определении ПФ разомкнутой цепи каждого из контуров нужно учитывать знак обратной связи, образующий этот контур.
3. Контуры не соприкасаются один с другим, когда у них нет ни общей координаты (стрелки на структурной схеме), ни общего звена (прямоугольника).
4. Каждая из функций ![]() вычисляется также, как и функция , но рассматривается лишь та часть структурной схемы, которая не соприкасается с i -и прямой цепью от х к у.
вычисляется также, как и функция , но рассматривается лишь та часть структурной схемы, которая не соприкасается с i -и прямой цепью от х к у.
5. Если со всеми прямыми путями соприкасаются все замкнутые контуры, а между собой замкнутые контуры также соприкасаются, то замкнутой системы можно определить по следующему правилу:
![]() есть отношение суммы произведений ПФ звеньев, образующих прямые пути от к у, к сумме единица плюс (минус) ПФ разомкнутых цепей всех замкну-тых контуров. Причем плюс при отрицательной обратной связи в контуре, минус — при положительной обратной связи.
есть отношение суммы произведений ПФ звеньев, образующих прямые пути от к у, к сумме единица плюс (минус) ПФ разомкнутых цепей всех замкну-тых контуров. Причем плюс при отрицательной обратной связи в контуре, минус — при положительной обратной связи.
Пример. В качестве примера рассмотрим определение ПФ замкнутой системы (рис. 3.11) по управлению.
1. ПФ прямых путей от g к х
2. ПФ разомкнутых цепей замкнутых контуров:
Все контуры соприкасаются друг с другом и со всеми прямыми путями.
4. Поскольку все контуры соприкасаются с прямыми путями, то
5. В соответствии с выражением (3.31) получим