Лекция 1. Задачи и метод сопротивления материалов. Растяжение и сжатие.
- Лекция 1. Задачи и метод сопротивления материалов. Растяжение и сжатие.
- Основные формы элементов конструкций
- Основные виды деформаций.
- Основные гипотезы науки о сопротивлении материалов.
- Напряжение
- Растяжение и сжатие
- Нормальные напряжения
- Испытания механических свойств материалов
- Деформации при растяжении (сжатии).
Центральным растяжением (сжатием) называется такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила (растягивающая и сжимающая) а все остальные внутренние силовые факторы равны нулю.
Растягивающие продольные силы принято считать положительными, а сжимающие — отрицательными.
Продольные силы определяются с помощью метода сечений.
Пример
Пусть имеется ступенчатый стержень, нагруженный силами ![]() ,
, ![]() и
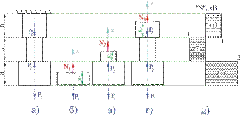
и ![]() вдоль оси стержня, показанного на рис. 11, а. Определить величину продольных сил.
вдоль оси стержня, показанного на рис. 11, а. Определить величину продольных сил.
Решение. Стержень может быть разделен на участки по местам приложения нагрузок и по местам изменения поперечного сечения.
Первый участок ограничен точками приложения сил ![]() и
и ![]() . Направим ось
. Направим ось ![]() вдоль оси участка вверх с началом координат в точке приложения силы
вдоль оси участка вверх с началом координат в точке приложения силы ![]() (начало первого участка). Мысленно рассечем первый участок поперечным сечением на расстоянии
(начало первого участка). Мысленно рассечем первый участок поперечным сечением на расстоянии ![]() от начала первого участка. Причем координата
от начала первого участка. Причем координата ![]() может быть взята в интервале
может быть взята в интервале ![]() , где
, где ![]() — длина первого участка.
— длина первого участка.
Рассмотрим равновесие нижней части стержня, заменив действие верхней части на нижнюю часть стержня продольной силой ![]() , предварительно направив ее в сторону растяжения рассматриваемой части.
, предварительно направив ее в сторону растяжения рассматриваемой части.
Из условия равновесия статики:
Положительный знак продольной силы говорит о том, что первый участок растянут.
Значение продольной силы не зависит от координаты ![]() , поэтому на всем участке значение продольной силы постоянно и равно
, поэтому на всем участке значение продольной силы постоянно и равно ![]() .
.
Рис. 11
Второй участок ограничен точками приложения сил ![]() и
и ![]() . Направим ось
. Направим ось ![]() вдоль оси участка вверх с началом координат в точке приложения силы
вдоль оси участка вверх с началом координат в точке приложения силы ![]() (начало второго участка).
(начало второго участка).
Мысленно рассечем второй участок поперечным сечением на расстоянии ![]() от начала второго участка. Причем координата
от начала второго участка. Причем координата ![]() может быть взята в интервале
может быть взята в интервале ![]() , где
, где ![]() — длина второго участка.
— длина второго участка.
Рассмотрим равновесие нижней части стержня, заменив действие верхней части на нижнюю часть стержня продольной силой ![]() , предварительно направив ее в сторону растяжения рассматриваемой части.
, предварительно направив ее в сторону растяжения рассматриваемой части.
Из условия равновесия статики:
Знак минус говорит о том, что второй участок сжат.
Аналогично для третьего участка :
Полученные результаты для большей наглядности удобней представить в виде графика (эпюры N), показывающего изменение продольной силы вдоль оси стержня. Для этого проводим нулевую (базовую) линию параллельно оси стержня, перпендикулярно которой будем в масштабе откладывать значения осевых усилий (рис. 1.11, д). В одну сторону откладываем положительные значения, в другую — отрицательные. Эпюра заштриховывается перпендикулярно нулевой линии, а в нутрии эпюры ставится знак откладываемой величины. Рядом указываются значения откладываемых величин. Рядом с эпюрой в кавычках указывается название эпюры («N») и через запятую — единицы измерения (кН)