Лекции для студентов

Лекции по метрологии. Часть 1: Основные понятия

 Измерение. Измеряемые величины

Определения метрологии и метрологического обеспечения на­чинаются с основного понятия — измерение. Пожалуй, ни одно определение в области метрологии не вызывает столько споров, как определение этого понятия. Профессором М. Ф. Маликовым было дано следующее определение: «Измерение — познавательный процесс, заключающийся в сравнении путем физического эксперимента данной величины с известной величиной, принятой за единицу сравнения». Недостатком этого определения является то, что оно предполагает сравнение измеряемой величины с ее единицей, что имеет место только при прямых измерениях с использованием метода сравнения с мерой. В частности, это определение не со­гласуется с косвенными измерениями. К.П.Широковым дано бо­лее общее определение: «Измерение — нахождение значения фи­зической величины опытным путем с помощью специальных тех­нических средств». Это определение, включенное в ГОСТ 16263-70, четко определяет границы самого понятия и содержит указания на все важнейшие его эле­менты. К тому же лаконичность этого определения является его до­стоинством. Предложения о включении в формулировку опреде­ления элементов терминологии кибернетики и теории информа­ции не опровергают стандартизированную формулировку, но усложняют ее понимание и запоминание. Следует отметить, что в нахождение значения физической величины (далее — величины) включается и математическая обработка результатов измерения, в частности введение поправок и статистическая обработка ре­зультатов наблюдений (если это требуется).

Значение величины, найденное путем его измерения, называется результатом измере­ния. Значение величины, полученное при отдельном измерении, называется результатом наблюдения (точнее — измерения). На­блюдением при измерении является экспериментальная операция, выполняемая в процессе измерений, в результате которой полу­чают одно значение из группы значений величины, подлежащих совместной обработке для получения результата измерения.

В определение понятия метрологического обеспечения входит термин «единство измерений», под которым понимается такое состояние измерений, при котором их результаты выражены в узаконенных единицах, размеры которых соответствуют едини­цам, воспроизводимым эталонами, погрешности результатов из­мерения известны с заданной вероятностью и не выходят за ус­тановленные пределы.

Этот термин позволяет обеспечить сопоставимость измерений, выпол­ненных в разное время, разными средствами и методами. Един­ство измерений обеспечивается единообразием средств измерений и правильностью методик их выполнения. При этом под едино­образием средств измерений понимается такое их состояние, при котором они градуированы в узаконенных единицах и их метро­логические свойства соответствуют установленным нормам.

Показателями качества измерений являются погрешность (точность), правильность, сходимость и воспроизводимость из­мерений.

Погрешность измерения — отклонение результата измерения от истинного значения измеряемой величины.

Точность измерений — их качество, отражающее близость их результатов к истинному значению измеряемой величины.

Правильность измерений — их качество, отражающее близость к нулю систематических погрешностей в их результатах.

Сходимость измерений — их качество, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях.

Воспроизводимость измерений — их качество, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях (в разное время, в различных местах, разными методами и средствами). Ниже будут рассмотрены более подробно все важнейшие элементы, необходимые для осуществления процесса измерений и обеспечения единства измерений [6].

Объектом измерения является физическая величина, характеризующая одно из свойств физического объекта.

Физическая величина, подлежащая измерению, измеряемая или измеренная в соответствии с основной целью измерительной задачи, называется измеряемой физической величиной или просто измеряемой величиной [3].

Измеряемые величины — это величины непосредственно воспринимаемые средствами измерений. Их можно классифицировать с помощью различных признаков, основными из которых являются: природа величины, вид отражаемой сто­роны эмпирических объектов, метризуемость и изменяемость [8].

По природе измеряемые величины разделяются на 11 классов: электрические, магнитные, электромагнитные, меха­нические, акустические, тепловые, оптические, химические, радио­активные, пространственные и временные. Каждый класс включает ко­нечное множество конкретных величин.

По виду отражаемой стороны эмпиричес­ких объектов каждый класс измеряемых величин разделяется на два подкласса: энергетические и вещественные величины. К энергетичес­ким величинам относятся, например, сила электрического тока, электрическое напряжение, напряженность электрического поля, на­пряженность магнитного поля, механическая сила, давление и т.п. Метрологическая общность энергетических величин заключается в использовании при их измерении энергии объектов исследования. Ве­щественными величинами являются различные свойства веществ и ма­териалов, а также параметры физических тел и объектов, например удельное электрическое сопротивление, диэлектрическая проницаемость, магнитная проницаемость, магнитное сопротивление, акустическое сопротивление и т.п. Метрологическая общность вещественных величин состоит в использовании при их измерении измерительных преобразо­ваний и других приемов косвенных измерений.

По признаку метризуемости измеряемые величины разделяются на непосредственно и косвенно метризуемые величины. К непосредственно метризуемым величинам относится около двух десятков физических величин, остальные являются косвенно метризуемыми величинами. Непосредственно метризуемые величины измеряются наиболее просто и с высокой точностью. Из­мерение косвенно метризуемых величин осуществляется с использованием различных функциональных связей и с преобразованием их в непосред­ственно метризуемые величины.

По признаку изменяемости выделяют состояния и измене­ния величин. Состояние величины в общем случае характеризуется раз­мером величины, нахождение значения которого и является задачей из­мерения.

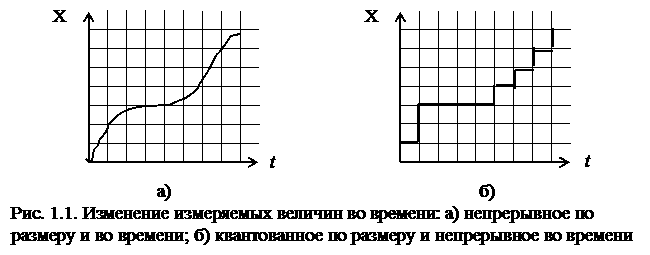
Изменение величины может происходить в пределах какого-либо диапазона размеров и во времени. В зависимости от числа размеров по диапазону различают непрерывные и квантованные по размеру изменения величин. При непрерывном по размеру изменении величины имеется бесконечное число размеров по диапазону. При ква­нтованном по размеру изменении величины в дан­ном диапазоне проявляется конечное число размеров величины.

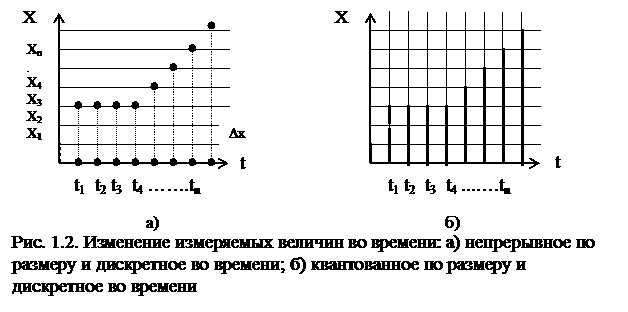
Изменение величины во времени может быть непрерывным и дискрет­ным (прерывным во времени). При непрерывном из­менении величины во времени значения размеров величины определены на данном отрезке времени при беско­нечно большом числе моментов времени. При дискретном из­менении величины значения размеров величины отлич­ны от нуля только в определенные моменты или интервалы времени. На рис. 1.1 и 1.2 показаны четыре характерные разновидности изменения величин.

Проявления размеров величины по диапазону и во времени могут быть неслучайными (детерминированными) и случайными. Детерми­нированное изменение величины характеризуется тем, что закон его известен. Случайное изменение величины происходит случайным образом.

Детерминированные непрерывные и дискретные изменения величин под­разделяются на периодические и непериоди­ческие. Непрерывные периодические и непериодические изменения величин далее подразделяются по виду описывающих их функций. Указанные из­менения величин характеризуются обобщенными параметрами и диапазо­нами их значений.

Для периодически изменяющейся величины x(t) любой формы с пе­риодом Т важными параметрами являются амплитудное x_m, среднее

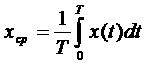и действующее 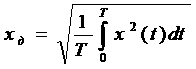значения, а также частота изменения величин. Непериодическое изме­нение величины

характеризуется максимальным значением, скоростью нарастания и скоростью спада.

Дискретные периодические и непериодические изменения величин подразделяются по форме импульса и характеризуются обобщенными параметрами (мгновенным, амплитудным, средним значениями, а также длительностью импульса, временем нарастания (спада) импульса, час­тотой следования) и диапазонами их значений.

Случайные непрерывные и дискретные изменения величин разделяют­ся на стационарные и нестационарные. При стационарном изменении величин, в отличие от нестационарного, закон распределения отдельных проявлений размеров не зависит от времени.

Случайные изменения величин описываются различными функциями (функцией распределения вероятностей, функцией плотности распреде­ления вероятностей, автокорреляционной функцией, спектральной плот­ностью и другими), каждая из которых может определяться вероятностя­ми и количеством реализации, а также диапазонами их значений.

Независимо от того, воспринимается состояние или изменение вели­чины измеряемой величиной, в любом конкретном случае может быть определено мгновенное значение раз­мера величины. При измерении состояния величины, т.е. не изменяющейся во времени величины или весьма медленно меняющейся, процесс измерения может осуществляться в течение длительного времени и к средствам измерения не предъявляется особых требований по быстродействию.

Измерение параметров изменений величин требует повышенного быст­родействия средств измерений. При этом помимо мгновенного значения размера величины в качестве измеряемой величины может выступать любой из указанных выше параметров изменений величин.

Различают истинное и действительное значения размера величины. Истинное значение размера величины есть значение размера величины, которое идеальным образом отражает количественную сторону соответствующего свойства объекта. Экспериментально определить его можно только в случае измерения количеств дискретных элементов каких-либо совокупностей, когда погрешность измерения практически может отсутствовать. Получить путем измерения истинное значение размера непрерывного изменения величины невоз­можно, так как в этом случае погрешности измерения неизбежны. Поэтому на практике часто вместо истинного пользуются действительным значением.

Действительное значение размера величина — это значение, найденное экспериментальным путем и настолько приближающееся к истинному, что может быть использова­но вместо него. Определяют его с помощью образцовых средств измере­ния, погрешностями которых по сравнению с используемыми при измере­нии средствами можно пренебречь.

  

• << Назад
• Вперёд >>