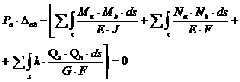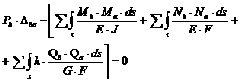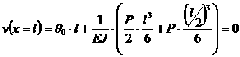Лекции для студентов

Лекция 9. Определение перемещений в упругих системах. Общие понятия

Теоремы о взаимности работ и перемещений

Запишем выражения начала возможных перемещений для балки, показанной на рис. 2.2.9, приняв для состояния в качестве возможных перемещения, вызванные состоянием , а для состояния  — перемещения, вызванные состоянием .

(2.2.21)

(2.2.22)

Так как выражения работ внутренних сил одинаковы, то очевидно, что

(2.2.23)

Полученное выражение носит название теоремы о взаимности работ (теоремы Бетти). Она формулируется следующим образом: возможная работа внешних (или внутренних) сил состояния на перемещениях состояния равна возможной работе внешних (или внутренних) сил состояния на перемещениях состояния .

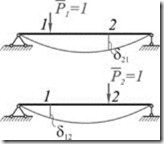
Применим теорему о взаимности работ к частному случаю нагружения, когда в обоих состояниях системы приложено по одной единичной обобщенной силе и .

Рис. 2.2.11

На основании теоремы о взаимности работ получаем равенство

, (2.2.24)

которое носит название теоремы о взаимности перемещений (теоремы Максвелла). Формулируется она так: перемещение точки приложения первой силы по ее направлению, вызванное действием второй единичной силы, равно перемещению точки приложения второй силы по ее направлению, вызванному действием первой единичной силы.

Теоремы о взаимности работ и перемещений существенно упрощают решение многих задач при определении перемещений.

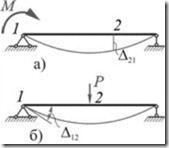
Пользуясь теоремой о взаимности работ, определим прогиб балки посредине пролета при действии на опоре момента (рис. 2.2.12, а).

Используем второе состояние балки — действие в точке 2 сосредоточенной силы . Угол поворота опорного сечения определим из условия закрепления балки в точке В:

Рис. 2.2.12

Согласно теореме о взаимности работ

,

откуда

(2.2.25)