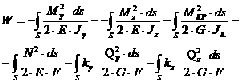Лекции для студентов

Лекция 9. Определение перемещений в упругих системах. Общие понятия

Работа внутренних сил.

Внутренние силы, возникающие при деформировании упругих систем, также совершают работу.

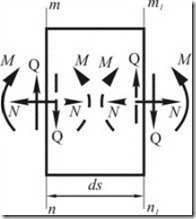
Рассмотрим элемент стержня длиной (рис. 2.2.6). В общем случае для плоского изгиба действие удаленных частей стержня на оставленный элемент выражается равнодействующими осевыми силами , поперечными силами и изгибающими моментами . Эти усилия, показанные на рис 2.2.6 сплошными линиями, по отношению к выделенному элементу являются внешними.

Рис.2.2.6

Внутренние силы, показанные штриховыми линиями, препятствуют деформации, вызываемой внешними силами, равны им по величине и обратны по направлению.

Вычислим работу, совершенную отдельно каждым внутренним силовым фактором.

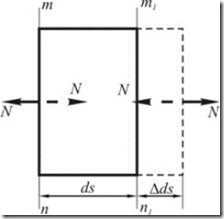
Пусть элемент испытывает только действие осевых усилий, равномерно распределенных по сечению (рис. 2.2.6).

Рис. 2.2.7

Удлинение элемента в результате этого

,

Работа, постепенно возрастающих от нуля до величины внутренних сил на этом перемещении.

. (2.2.8)

Работа внутренних сил отрицательна, поэтому в полученной формуле стоит знак «минус».

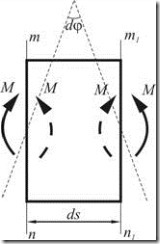
Рассмотрим теперь элемент, находящийся под действием изгибающих моментов (рис. 2.2.8).

Взаимный угол поворота сечений элемента

.

Работа изгибающих моментов

. (2.2.9)

Рис. 2.2.8

Работу постепенно возрастающих внутренних поперечных сил с учетом распределения касательных напряжений по поперечному сечению и на основании закона Гука можно записать в следующем виде

, (2.2.10)

где  — коэффициент, зависящий от формы поперечного сечения.

Если стержень подвергается кручению, элементарная работа постепенно возрастающих крутящих моментов

(2.2.11)

Наконец в общем случае действия на брус в сечениях имеем шесть внутренних силовых факторов, работу которых можно определить по формуле

(2.2.12)

• << Назад
• Вперёд >>