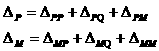Лекции для студентов

Лекция 9. Определение перемещений в упругих системах. Общие понятия

Страница 1 из 5

Определение перемещений в упругих системах. Общие понятия

Обобщенные силы и перемещения

Ранее нами были рассмотрены некоторые частные способы определения перемещений, удобные при решении простейших задач.

Начало возможных перемещений и закон сохранения энергии позволили получить другие методы определения перемещений в стержневых системах.

Как известно из теоретической механики, работа постоянной силы на перемещении по ее направлению равна произведению величины силы на указанное перемещение:

В задачах сопротивления материалов и строительной механики внешняя нагрузка отличается большим разнообразием и обычно представляет собой группы сил. Выражение для работы группы постоянных сил также можно представить в виде произведения двух величин

, (2.2.1)
в котором множитель зависит только от сил группы и называется обобщенной силой, а зависит от перемещений и называется обобщенным перемещением.

Таким образом, под обобщенной силой будем понимать любую нагрузку (сосредоточенные силы, сосредоточенные пары, распределенную нагрузку), а под обобщенным перемещением — тот вид перемещения, на котором обобщенная сила производит работу.

Рассмотрим некоторые примеры часто встречающихся обобщенных сил и обобщенных перемещений.

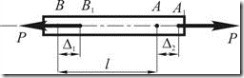
1. На рис. 2.2.1 показана обобщенная сила, состоящая из двух равных по величине противоположных сил , приложенных в точках и и направленных по одной прямой. Предположим. Что точки приложения сил и переместились в направлении на отрезки и . Очевидно, работа системы постоянных сил на этих перемещениях

, (2.2.2)

где — изменение расстояния между точками приложения сил.

Рис. 2.2.1

Следовательно, в данном случае — обобщенная сила, а изменение длины отрезка — обобщенное перемещение.

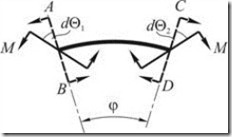
2. Пусть группа сил состоит из двух пар сил, момент каждой из которых (рис. 2.2.2). Допустим, что элемент повернулся на угол , а элемент на угол .

Рис. 2.2.2

Легко убедиться, что обобщенной силой является момент пары , а обобщенным перемещением — изменение угла между элементами и :

Рассматривая достаточно жесткие конструкции, деформации которых следуют закону Гука, можно на основании принципа независимости действия сил определить полные перемещения точек как сумму перемещений, вызванных отдельными нагрузками.

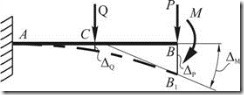
Рис. 2.2.3

Для показанной на рис. 2.2.3 балки прогиб и угол поворота сечения можно записать в виде

(2.2.3)

где — полное перемещение сечения в направлении действия силы ;

— перемещение сечения в направлении действия силы от действия силы ;

— перемещение сечения в направлении действия силы от действия момента ;

— полное перемещение сечения по направлению пары (угол поворота).

— перемещение сечения в направлении действия пары от действия силы ;

— перемещение сечения в направлении действия пары от действия пары ;

Перемещение, вызванное единичной силой () или единичной парой (), будем обозначать буквой и называть удельным. При этом условимся считать единичные силы и единичные пары, вызывающие перемещения , безразмерными.