Лекции для студентов

Лекция 9. Определение перемещений в упругих системах. Общие понятия

Работа внешних сил.

При деформации конструкций происходит перемещение точек приложения внешних сил, при этом внешние силы на заданных перемещениях совершают работу.

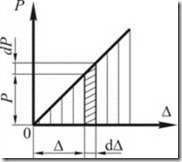
Вычислим работу некоторой обобщенной силы (рис. 2.2.4), которая возрастает от нуля до заданной величины достаточно медленно, чтобы можно было пренебречь силами инерции перемещаемых масс. Такую нагрузку принято называть статической.

Рис.2.2.4

Пусть в произвольный момент деформации силе соответствует обобщенное перемещение . Бесконечно малое приращение силы на величину вызовет бесконечно малое приращение перемещения . Очевидно, что элементарная работа внешней силы, если пренебречь бесконечно малыми величинами второго порядка,

Полная работа, совершенная статически приложенной обобщенной силой , вызвавшей обобщенное перемещение ,

. (2.2.5)

Полученный интеграл представляет собой площадь диаграммы , которая для линейно деформированных систем является площадью треугольника с основанием окончательного значения перемещения и высотой окончательного значения силы

(2.2.6)

Рис. 2.2.5

Таким образом, действительная работа при статическом действии обобщенной силы на упругую систему равна половине произведения окончательного значения силы на окончательное значение соответствующего ей обобщенного перемещения (теорема Клапейрона).

В случае статического действия на упругую систему нескольких обобщенных сил работа деформаций равна полусумме произведений окончательного значения каждой силы на окончательное значение соответствующего суммарного перемещения

(2.2.7)

и не зависит от порядка нагружения системы.

• << Назад
• Вперёд >>