Лекции для студентов

Лекции по метрологии. Часть 3: Средства измерений

 Измерительные приборы

Измерительный прибор — средство измерения, предназначен­ное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем.

Выработка измерительной информации может основываться на использовании различных физических принципов. Например, для из­мерения длины применяют механические, оптические, пневмати­ческие и электрические измерительные приборы.

Физический принцип, положенный в основу построения изме­рительного прибора, называют принципом действия прибора, кото­рый часто отражается в названии прибора, например, электро­динамический ваттметр, термоэлектрический термометр.

Принципиально измерительный прибор состоит из ряда изме­рительных преобразователей, каналов связи, согласующих эле­ментов, измерительного механизма, которые в совокупности образу­ют измерительную цепь прибора. Измерительная цепь осуществ­ляет все преобразования сигнала измерительной информации.

Измерительная цепь начинается чувствительным элементом, яв­ляющимся составной частью первичного преобразователя. На эле­мент непосредственно воздействует измеряемая величина. Оканчи­вается цепь отсчетным устройством, с помощью которого наблюда­тель определяет значение измеряемой величины, выраженное в принятых единицах измерения. Это значение называют показанием средства измерения, которое образуется от отсчета (отвлеченного числа), снятого при измерении с отсчетного устройства прибора. Переход от отсчета к показанию осуществляется умножением от­счета на цену деления шкалы, под которой понимается разность значений величины, соответствующих двум соседним отметкам шкалы.

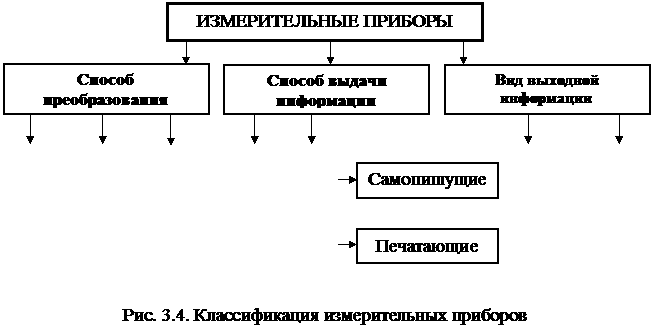
Измерительные приборы можно классифи­цировать по различным признакам: структуре преобразования; ви­ду выходной информации; способу ее выдачи; роду измеряемой величины; условиям применения и т.д.

Классификация измерительных приборов с учетом этих признаков представлена на рис. 3.4.

        Измерительные приборы по своей структуре представляют со­бой определенное сочетание измерительных преобразователей и устройства сравнения. Для условного изображения структуры прибора используется функциональная схема. По ней можно проследить все преобразования, которым

подвергается измеряемая величина в процессе работы прибора.

       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

        По структуре преобразования все измерительные приборы можно разделить на три вида: приборы прямого преобразования, приборы уравновешивающего  преобразования и приборы смешанного преобразования.

        Средства измерений прямого преобразования. Структурная схема прибора  прямого  пре­образования  показана  на рас. 3.5, где ИП₁, ИП₂,…,ИП_n -звенья; х, х₁, х₂,..., х_n — информатив­ные параметры сигналов.

 

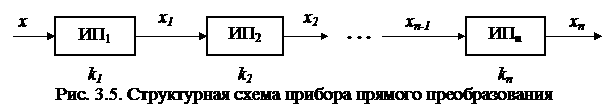Как видно из рис. 3.5, входной сигнал х последовательно претерпевает несколько преобразований и в итоге на выходе получается сигнал х_n .

Для измерительного прибора сигнал x_n получается в форме, доступной для непосредственного восприятия наблюдателем, на­пример, в виде отклонения указателя отсчетного устройства. Для измерительного преобразователя сигнал х_n получается в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения.

Примером электроизмерительного прибора, имеющего струк­турную схему прямого преобразования, может быть амперметр для измерения больших постоянных токов. В этом приборе изме­ряемый ток вначале с помощью шунта преобразуется в падение напряжения на шунте, затем в малый ток, который измеряется измерительным механизмом, т.е. преобразуется в отклонение указателя [11].

        Структурная схема прибора прямого преобразования ра­зомкнутая, в ней отсутствует общая обратная связь с выхода на вход. Если все измерительные преобразователи имеют линейную функцию преобразования (х_i = k_i×х_i-1 ), то выходная величина связана с измеряемой величиной соотношением

                                                     х_n = k₁×k₂¼k_n×x = k×x ,                                        (3.1)

где  k₁ , k₂ ,¼, k_n  -   коэффициенты преобразования измери­тельных преобразователей.

Чувствительность (коэффициент преобразования) средства измерений, имеющего структурную схему прямого преобразо­вания:

                                            k₁×k₂×k₃¼k_n .                      (3.2)

При нелинейной функции преобразо­вания чувствительность и коэффициенты преобразования зави­сят от входного сигнала.

Мультипликативная погрешность возникает при изменении коэффициентов преобразования. С течением времени и под дей­ствием внешних факторов коэффициенты k₁, k₂, k₃ ,¼, k_n могут изме­няться соответственно на Dk₁, Dk₂, Dk₃ ,¼, Dk_n. При достаточно малых изменениях этих коэффициентов можно пренебречь членами вто­рого и большего порядков малости,  тогда относительное измене­ние чувствительности

                                              .                                          (3.3)

Изменение чувствительности приводит к изменению выходно­го сигнала на Dx_n = (S + DS)×x - S×x=DS×x . Этому изменению вы­ходного сигнала соответствует абсолютная погрешность измере­ния входной величины

                                                     .                                                 (3.4)

Как видно из выражения (3.4), погрешность, вызванная изменением чувствительности, является мультипликативной. От­носительная мультипликативная погрешность измерения  d_ь = DS/S .

Аддитивная погрешность вызывается дрейфом «нуля» звень­ев, наложением помех на полезный сигнал и т.д., приводящих к смещению графика характеристики преобразования i-гo звена на ±Dx_0i; (как показано на рис. 3.6). Аддитивную погрешность можно найти, введя на структурной схеме после соответствующих звеньев дополнительные внешние сигналы Dx₀₁ , Dx₀₂, …, Dx_0n , равные смещениям характеристик преобразования звеньев.

Для оценки влияния этих дополнительных сигналов пересчи­таем (приведем) их ко входу структурной схемы. Результирующее действие всех дополнительных сигналов равно действию следу­ющего дополнительного сигнала на входе:                    .                          (3.5)

Результирующая аддитивная погрешность равна Dx₀. Таким образом, как следует из (3.3) и (3.5), в средствах измерений, имеющих структурную схему прямого преобразования, происхо­дит суммирование погрешностей, вносимых отдельными звень­ями, и это затрудняет изготовление средств измерений прямого преобразования с высокой точностью.

 

 

Средства измерений уравновешивающего преобразования. Структурная схема средства измерений уравновешивающего преобразования показана на рис. 3.7.

 
 

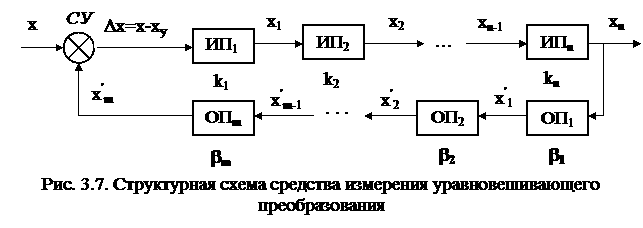Структурная схема такого прибора содержит две цепи  — цепь прямого преобразования и цепь обратного преобразования, т.е. в приборе имеется общая отрицательная обратная связь с выхода на вход.

Для цепи обратного преобразования (обратной связи)

                                             x^¢_m = x_n×b₁×b₂×…×b_m = x_n× b  ,                                     (3.6)

где b  - коэффициент преобразования цепи обратного преобразо­вания; b₁, b₂, …, b_m - коэффициенты преобразования звеньев обратной связи.

На входе цепи прямого преобразования в узле СУ происходит сравнение (компенсация) входного сигнала х и выходного сигна­ла цепи обратного преобразования х'_m  и при этом на выходе СУ получается  разностный  сигнал Dх = х—х'_m .

При подаче на вход сигнала х выходной сигнал x_n , а следова­тельно, и х'_m , будут возрастать до тех пор, пока х и х'_m не станут равны. При этом по значению x_n можно судить об измеряемой величине х.

Средства измерений, имеющие такую структурную схему, могут работать как с полной, так и с неполной компенсацией.

При полной компенсации (астатическое преобразование) в установившемся режиме                                      Dх = х—х'_m =0 .                                                    (3.7)

Это возможно в тех устройствах, у которых в цепи прямого преобразования предусмотрено интегрирующее звено с характеристикой преобразования 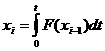. Примером такого звена является электродвигатель, для которого угол поворота вала определяется приложенным напряжением и временем.

В этом случае, учитывая (3.6) и (3.7), получим

                                                  x_n = x/(b₁×b₂…b_m) = x/b .                                       (3.8)

        Таким образом, в момент компенсации сигнал на выходе средства измерений пропорционален входному сигналу и не за­висит от коэффициента преобразования цепи прямого преобра­зования.

Чувствительность (коэффициент преобразования)

                                         .                                         (3.9)

Мультипликативная относительная погрешность, обуслов­ленная нестабильностью коэффициентов преобразования звень­ев, при достаточно малых изменениях этих коэффициентов

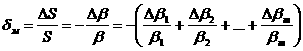                               .                      (3.10)

Как видно из этого выражения, относительная мультиплика­тивная погрешность обусловлена только относительным измене­нием коэффициента преобразования цепи обратного преобразо­вания.

Аддитивная погрешность в средствах измерений с полной компенсацией практически обусловливается порогом чувстви­тельности звеньев, расположенных до интегрирующего звена, и порогом чувствительности самого интегрирующего звена.

Под порогом чувствительности звена понимается то наимень­шее изменение входного сигнала, которое способно вызвать по­явление сигнала на выходе звена. Порог чувствительности имеют, например, электродвигатели, часто применяемые в рассматрива­емых устройствах. Для реальных звеньев график характеристики преобразования может иметь вид, как показано на рис.3.8, где  ± Dх _i-1  — порог чувствительности.

 

Порог чувствительности средства измерений с полной ком­пенсацией                          ,            (3.11)

где Dx₁, Dx₂ , … , Dx_i-1 -   пороги чувствительности

звеньев цепи прямого преобразования; Dx_i — порог чувствительности интегри­рующего звена.

При наличии порога чувствительности средства измерении состояние компенсации наступает при х — х'_m =Dх. Таким обра­зом, изменение входного сигнала в пределах ±Dx не вызывает изменения выходного сигнала, т.е. появляется абсолютная ад­дитивная погрешность, значение которой может быть в пределах ±Dx.

Из выражения (3.11) очевидно, что для уменьшения аддитив­ной погрешности, обусловленной порогом чувствительности звеньев, следует увеличивать коэффициенты преобразования k₁ , k₂ , ..., k_i-1. Предел увеличения этих коэффициентов обусловлен динамической устойчивостью средства измерений.

При неполной компенсации  (статическое преобразование) в средствах измерений интегриру­ющего звена нет и обычно выполняется условие (3.6), а также

                                                              x_n = k×Dx,                                                (3.12)

где k=k₁× k₂ ... k_n  - коэффициент преобразования цепи прямого преобразования. В этом случае установившийся режим наступа­ет при некоторой разности

                                                    Dх = х—х'_m                                                     (3.13)

Зависимость между выходным и входным сигналами, находи­мая путем решения уравнений (3.6), (3.12) и (3.13),

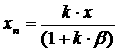                                                                                              (3.14)

Как видно из выражения (3.14), при установившемся режиме выходной сигнал пропорционален входному и зависит от коэффициентов цепи как обратного, так и прямого пре­образования.

Если выполняется условие k×b » 1, то уравнение (3.14) пе­реходит в (3.8) и при этом нестабильность коэффициента пре­образования цепи прямого преобразования не влияет на работу устройства. Практически, чем выше k×b , тем меньше влияние k. Предел увеличения k×b  обусловлен динамической устойчиво­стью средства измерений.

Чувствительность (коэффициент преобразования) средства измерений с неполной компенсацией

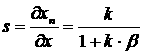                                            .                                            (3.15)

Мультипликативная погрешность, обусловленная изменением коэффициентов преобразования звеньев при достаточно малых изменениях этих коэффициентов:

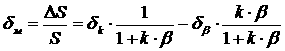                                 ,                        (3.16)

где d_k = Dk/k;  d_b = Db/b. Если k×b » 1, то d_м » d_k/k×b . Следо­вательно, при k×b » 1 (что обычно имеет место) составляющая, обусловленная изменением коэффициента b, целиком входит в ре­зультирующую погрешность, а составляющая, обусловленная изменением коэффициента k, входит в результирующую погреш­ность ослабленной в k×b  раз. Нелинейность характеристики преобразования цепи прямого преобразования можно рассматривать как результат влияния изменения коэффициента преобразования k относительно некото­рого начального значения при х=0. Полученные уравнения пока­зывают, что нелинейность характеристики преобразования уменьшается действием отрицательной обратной связи в k×b  раз.

Аддитивная погрешность может быть найдена путем введе­ния в структурную схему дополнительных сигналов Dx₀₁, Dx₀₂,…, Dx_0n, Dx^¢₀₁, Dx^¢₀₂,…, Dx^¢_0m , равных смещениям характеристик преобразования соответствующих звеньев.

Применяя методику, рассмотренную выше, получим абсолют­ную аддитивную погрешность, равную погрешности:

 

 

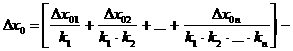
Следует отметить, что средства измерений могут иметь комби­нированные структурные схемы, когда часть цепи преобразова­ния охвачена обратной связью.

Вид структурной схемы средства измерений влияет не только на рассмотренные характеристики (чувствительность, погреш­ность), но также на входные и выходные сопротивления, динами­ческие свойства и др.

По виду выдаваемой информации все приборы делятся на аналоговые и цифровые. Аналоговым является измерительный прибор, показания которого являются не­прерывной функцией измеряемой величины, например,  стрелочный вольтметр. Цифровым называется измерительный прибор, автоматически вырабатывающий дискретные сигналы измерительной информации, показания которого представлены в цифровой форме, например,  цифровой омметр.

По способу выдачи измерительной информации измерительные приборы делятся на показывающие и регистрирующие (см. рис. 3.4).

Показывающие приборы (рис. 3.9), если на них воздействует измеряемая величина, допускают только отсчитывание показаний. Указатель      отсчетного

 

устройства перемещается относительно шкалы и наблю­дается визуально. Шкала средства измерения — это часть отсчет­ного устройства, представ-ляющая собой совокупность отметок и проставленных у некоторых из них чисел отсчета или других символов, соответ-ствующих ряду последователь-ных значений из­меряемой величины.

Шкалы с делениями постоянной длины и с постоянной ценой деления называются равномерными шкалами, а шкалы с делени­ями непостоянной длины — неравномерными.

Примерами показывающих приборов со шкалами могут служить следующие типы приборов: 1) электромеханические: М2027, М2042, ЭА2231;  2) электронные: В3-38, В2-25, В7-13 и др.

 

К показывающим измерительным приборам относят также приборы с цифровым отсчетом (рис.3.10). Их отсчетное устройство выдает показания в цифровой форме, показанное число соответствует значению изме­ряемой величины.

 

 

Измерительные приборы с цифровым отсчетом находят все большее распространение, поскольку они более производительны и удобны для наблюдателя. Примерами показывающих приборов с цифровым отсчетом могут служить следующие типы приборов: В2-37, Щ4310, Ч3-34, В7-22, В7-21 и др.

Регистрирующие измерительные приборы (рис.3.11) содержат механизм регистрации показаний. Регистрирующий прибор, в котором преду­смотрена запись показаний в форме диаграммы, называют самопи­шущим прибором.

К регистрирующим следует отнести измерительные приборы с печатающими механизмами, дающими показание в виде чисел, от­печатанных на бумажной ленте. Примерами регистрирующих приборов могут служить следующие типы приборов: Н30, Н32, Н310, Н3140 и др.

По роду измеряемой величины приборам присвоены наименования в зависимости от названия единицы этой величины (в том числе кратных и дольных единиц), для измерения которой они предназначены: амперметры, микроамперметры  — для измерения тока; веберметры, милливеберметры  — для измерения магнитной индукции и т.д.