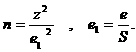Лекции для студентов

Маркетинговые исследования. Часть 2

10.3. Определение объема выборки

 

На практике решение вопроса об объеме выборки является компромиссным между предположением о точности результатов обследования и возможностями их практической реализации (т.е. исходя из затрат на проведение опроса).

На практике используется несколько подходов к определению объема выборки. Обратим внимание на самые простые из них. Первый из них называется произвольным подходом и основан он на применении «правила большого пальца».

Например, бездоказательно принимается, что для получения точных результатов выборка должна составлять 5 % от совокупности. Данный подход простой и доступный в исполнении, не позволяет получать точные результаты. Его достоинством является относительная дешевизна затрат. В соответствии со вторым подходом объем выборки может быть установлен исходя из заранее оговоренных условий. Заказчик маркетингового исследования, например, знает, что при изучении общественного мнения выборка обычно составляет 1000 — 1200 человек, поэтому он рекомендует исследователю придерживаться данной цифры.

Третий подход означает, что в некоторых случаях главным аргументом при определении объема выборки может быть стоимость проведения опроса. Хотя при этом ценность и достоверность получаемой информации не принимается в расчет.

В случае четвертого подхода объем выборки определяется на основе статистического анализа. Данный подход предполагает определение минимального объема выборки с учетом требований к надежности и достоверности получаемых результатов.

Пятый подход считается наиболее теоретически обоснованным и правильным подходом в определении объема выборки. Он основан на расчете доверительного интервала.

Доверительный интервал — это диапазон, крайние точки которого характеризуют процент определенных ответов на какой-то вопрос. Данное понятие тесто связано с понятием «среднее квадратичное отклонение получаемого признака в генеральной совокупности». Чем оно больше, тем шире должен быть доверительный интервал, чтобы включить в свой состав, например 9,5 % ответов.

Из свойств нормальной кривой распределения вытекает, что конечные точки доверительного интервала, равного к примеру 9,5 % определяются как произведение: 1,96 (нормированное отклонение) и среднего квадратичного отклонения.

Числа 1,96 и 2,58 (для 99 % доверительного интервала) обозначаются как z.

Существуют таблицы «Значение интеграла вероятности», которые дают возможность определить величины z для различных доверительных интервалов. Доверительный интервал равный 95% или 99% является стандартным при проведении маркетинговых исследований.

Например, проведено исследование числа визитов автовладельцев в сервисные мастерские за год. Доверительный интервал для среднего числа визитов был рассчитан равным 5 — 7 визитам при 99 % уровне доверительности. Это означает, что если появится возможность, провести независимо 100 раз выборочные исследования, то для 99 выборочных исследований среднее значение числа визитов попадут в диапазон от 5 до 7 визитов, Если сказать иначе, то 99 % автовладельцев попадут в доверительный интервал.

Допустим, было проведено исследование до 50 независимых выборок. Средние оценки для этих выборок образовали нормальную кривую распределения, которое называется выборочным распределением.

Средняя оценка для совокупности в целом равна средней оценке кривой распределения. Понятие «выборочное распределение» рассматривается также в качестве одного из базовых понятий теоретической концепции, лежащее в основе определения V выборки.

Естественно ни одна компания не в состоянии сформировать 10, 20, 50 независимых выборок. Обычно используется только одна выборка.

Математическая статистика позволяет получить некую информацию о выборочном распределении, владея точными данными о вариации единственной выборки.

Индикатором степени отличия оценки, истинной для совокупности в целом, которая ожидается для типичной выборки, является средне квадратическая ошибка. К примеру, исследуется мнение потребителей о новом товаре и заказчик данного исследования указал, что его устроит точность полученных результатов, равная плюс минус 5%.

Предположим, что 30 % членов выборки высказались за новый продукт. Это означает, что диапазон возможных оценок для всей совокупности составляет 25 — 35 %. Причем, чем больше объем выборки, тем меньше ошибка. Высокое значение вариации обусловливает высокое значение ошибки и наоборот.

Определим объем выборки на основе расчета доверительного интервала. Исходной информацией, необходимой для реализации данного подхода, является:

· величина вариации, которой, как считается, обладает совокупность;

· желаемая точность;

· уровень достоверности, которому должны удовлетворять результаты проводимого обследования.

Когда на заданный вопрос существует только два варианта ответов, выраженных в процентах (используется процентная мера), объем выборки определяется по следующей формуле:

,

где n — объем выборки;

z — нормированное отклонение, определяемое исходя из выбранного уровня доверительности (табл. 7);

р — найденная вариация для выборки;

q = (100 — p);

е — допустимая ошибка.

Таблица 7

Значение нормированного отклонения оценки z от среднего значения

в зависимости от доверительной вероятности (а) полученного результата

а, %	60	70	80	90	90	95	97	99,0	99,7
z	0,84	1,03	1,29	1,44	1,65	1,96	2,18	2,58	3,0

Например, предприятием, выпускающим покрышки, проводится опрос автолюбителей, использующих радиальные покрышки.

Поэтому на вопрос: «Используете ли Вы радиальные покрышки?» возможны только 2 ответа: «Да» или «Нет». Если предположить, что совокупность автолюбителей обладает низким показателем вариации, то это означает, что почти каждый опрошенный использует радиальные покрышки. В данном случае может быть сформирована выборка достаточно малых размеров. В формуле (1) произведение pg выражает вариацию, свойственную совокупности. Например, пусть 90 % единиц совокупности используют радиальные покрышки. Это означает, что pg = 900. Если принять, что показатель вариации выше (р = 70 %), то pg = 2100. Наибольшая вариация достигается в случае, когда одна половина совокупности (50 %) использует радиальные покрышки, а другие не используют. В этом случае произведение достигает значения равного 2500.

При проведении опроса важно указывать точность полученных оценок. Например, было установлено, что 44 % респондентов используют радиальные покрышки. Результаты измерения необходимо представить в виде: процент автолюбителей, использующих радиальные покрышки, составляет 44 плюс — минус е %. Величина допустимой ошибки заранее совместно определяется заказчиком исследования и исполнителем.

Уровень достоверности при проведении маркетинговых исследований обычно оценивается с учетом двух его значений: 95% или 99%. Первому значению соответствует значение z = 1,96; второму — z = 2,58. Если выбирается уровень доверительности равный 99 %, то это говорит о следующем: мы уверены на 99 % (иными словами доверительная вероятность равна 0,99) в том, что процент членов совокупности, попавший в диапазон плюс — минус е %, равен проценту членов выборки, попавших в тот же диапазон ошибки. Принимая вариацию равной 50 %, точность равной 10 % при 95 %-м уровне доверительности рассчитаем размер выборки:

n = 1,96² (50 х 50) / 10² = 96.

При уровне доверительности равном 99 %, и е = ±3 %, n = 1067.

При определении показателя вариации для конкретной совокупности целесообразно проводить предварительно качественный анализ исследуемой совокупности и установить схожесть единиц совокупности в демографическом, социальном и других отношениях, представляющих интерес для исследователя. Возможно определение объема выборки на основе использования средних значений, а не процентных величин. Предположим, что выбран уровень достоверности равный 95 % (z = 1.96,), среднеквадратическое отклонение (S) рассчитано и равно 100, и желаемая точность (погрешность) составляет ±10. Тогда объем выборки составит

Реально на практике, если выборка формируется заново и схожие опросы не проводились, S неизвестно.

В этом случае целесообразно задавать погрешность е в долях от среднеквадратического отклонения. Расчетная формула преобразуется и приобретает следующий вид:

Мы в основном говорили о совокупности очень больших размеров, характерных для рынков потребительских товаров. Но в отдельных случаях совокупности не являются столь большим, и например на рынках отдельных видов продукции производственного назначения.

Обычно, если выборка составляет менее 5 % совокупности, то совокупность считается большой, и расчеты проводятся по вышеприведенным правилам.

Если же V выборки превышает 5 % совокупности, то последняя считается малой, и в вышеприведенные формулы вводится поправочный коэффициент. Объем выборки в данном случае определяется следующим образом:

,

где n¹ – объем выборки для малой совокупности,

n — объем выборки (или для процентных мер или для средних), рассчитанный по приведенным выше формулам,

N — объем генеральной совокупности.

Например, изучается мнение членов совокупности, состоящей из 1000 компаний, относительно строительства химического комбината в границах города Томска. Вследствие отсутствия информации о вариации принимается наихудший случай: 50:50. Исследователь вынес решение использовать уровень доверительности равный 95 %. Заказчик исследования указал, что его устроит точность результатов плюс минус 5 %. В этом случае используется следующая формула для процентной меры:

Данный подход к формированию V выборки с определенными оговорками может быть использован и при расчете численности панели и экспертной группы.

Приведенные формулы расчета выборки основаны на предположении, что все правила формирования выборки были соблюдены, и единственной ошибкой является ошибка, обусловленная ее объемом.

 

Контрольные вопросы и задания

1. Дайте определение понятия «генеральная совокупность».

2. Определите понятия: «выборка», «ошибка выборки», «контур выборки».

3. Чем отличается вероятностная выборка от невероятностной?

4. Что является единицей выборки?

5. Раскройте содержание метода простого случайного отбора.

6. В чем особенности метода систематического отбора в выборку?

7. Дайте характеристику метода кластерного отбора.

8. Раскройте специфику метода стратифицированного отбора.

9. Перечислите невероятностные методы отбора выборки?

10. Перечислите основные этапы проектирования выборки и охарактеризуйте их.

11. Раскройте сущность основных методов формирования повторной выборки.

12. Охарактеризуйте основные подходы к определению объема выборки.

13. Дайте определение доверительного интервала.

14. По каким формулам определяется объем выборки?